Rational numbers
Fractional negative numbers. Positive numbers.
Rational numbers.
Negative integers appear, when the greater integer is subtracted from the smaller one, for instance:
10 – 15 = – 5 .
The sign “minus” before 5 shows, that this number is negative.
Series of negative integers continue endlessly:
–1, –2, –3, – 4, –5, …
Integers are natural numbers, negative integers and zero:
... , –3, –2, –1, 0, 1, 2, 3, ...
Fractional negative numbers appear, for example, when the greater number is subtracted from the smaller one:
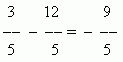
Also it is possible to say, that fractional negative numbers appear as a result division of a negative integer by a natural number:
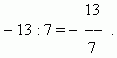
Positive numbers in contrast to negative numbers (integers and fractional ones), are the numbers, considered in arithmetic (also integers and fractional ones).
Rational numbers – positive and negative numbers (integers and fractional ones) and zero. The more exact definition of rational numbers, adopted in mathematics, is the following:
A number is called rational , if it may be presented as a vulgar, not a cancelled fraction of the shape: m / n , where m is an integer, and n is a natural number.