Arithmetical root

As we know, an even degree root has two values: positive and negative, so

An arithmetical root of the n -th degree of a non-negative number a is called a non-negative number, the n -th power of which is equal to a .

An algebraic root of the n -th degree of a given number a iscalled a set of all roots of this number. An algebraic root of an even degree has the two values:positive and negative, for instance:

An algebraic root of an odd degrees has a single value: either positive, or negative.For example, the arithmetical root

Unlike this, the cube degree root:

An arithmetical root is closely connected with the notion of an absolute value(modulus) of number, exactly:

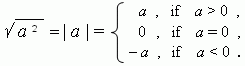
Operations with roots in more detail see the section “Powers and roots” .