Linear equations in one unknown
An equation of the shape: ax + b = 0, where a and b – the known numbers, x – an unknown value, is called a linear equation in one unknown. To solve this equation means to find the numerical value of x , at which this equation becomes an identity.
If a is not equal to zero ( a ≠ 0 ), then a solution ( root ) has the shape:
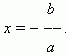
If a = 0 , then the two cases are possible:
1 . b = 0, then 0 · x + 0 = 0 . Here x can be any number ( check this ! ).
2 . b ≠ 0, then 0 · x + b = 0 . There is no solution ( check this also ).
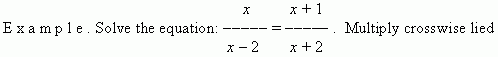
expressions:
x
2
+
2
x = x
2
–
2
x
+ x –
2
.
Transfer all terms to the
left-hand side of the equation. After reducing all similar terms we’ll
receive: 3 x + 2 = 0, hence x = – 2 / 3 .