Systems of two simultaneous linear equations in two unknowns

Systems of two simultaneous linear equations in two unknowns have the shape:

where a, b, c, d, e, f – numerical coefficients; x, y – unknowns.

Solution of these simultaneous equations can be found by two basic methods:

Substitution. 1). From one equation we express one of unknowns, for example x , by coefficients and another unknown y :

x = ( c – by ) / a , (2)

2). Substitute in the second equation instead of x :

d ( c – by ) / a + ey = f .

3). Now, solving the last equation, find y :

y = ( af – cd ) / ( ae – bd ).

4). Substitute this value for y in the expression (2) instead of y :

x = ( ce – bf ) / ( ae – bd ) .

E x a m p l e .  Solve the system of simultaneous equations:

From the first equation express x by coefficients and y :

x = ( 2 y + 4 ) / 3 .

Substitute this expression into the second equation and find y :

( 2 y + 4 ) / 3 + 3 y = 5 , hence y = 1 .

Now find x , substituting the found value instead of y into

expression for x : x = ( 2 · 1 + 4 ) / 3 , from here x = 2 .

Addition or subtraction. This method consists in the following.

1).  Multiply both sides of the first equation of the system (1) by ( – d ) and both sides

of the second equation by a and add them:

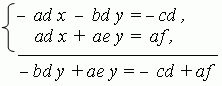
From here we receive: y = ( af – cd ) / ( ae – bd ) .

2).  Substitute the found value of y into any equation of the original system (1) :

ax + b( af – cd ) / ( ae – bd ) = c .

3).  Find another unknown x : x = ( ce – bf ) / ( ae – bd ) .

E x a m p l e . Solve the system of simultaneous equations:

by the second way  ( addition or subtraction ).

Multiply the first equation by  –1,  the second by 3 and add them:

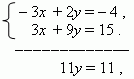
From here y = 1 . Substitute this value into the second equation

( is it possible to substitute this into the first equation ? ): 3 x + 9 = 15, hence, x = 2 .

The second order determinants. We saw, that formulas for solution of the system of two simultaneous linear equations in two unknowns have the shape:

x = ( ce – bf ) / ( ae – bd ) ,

(3)

y = ( af – cd ) / ( ae – bd ) .

These formulas can be remembered very easily, if to introduce for their numerators and denominators the next symbol:

,  which will be used to mean an expression:  ps – qr .

This expression is received by crosswise multiplication of numbers p , q , r , s :

and the following subtraction of one product from another: ps – qr. The sign  “+” is taken for a product of numbers, located on the diagonal, going from the left upper number to the right lower number. The sign “ – “ for another diagonal, going from the right upper number to the left lower number. For example,

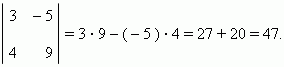
The expression 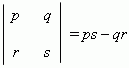is called the second order determinant .

Cramer’s rule. Using the determinants, the formulas (3) can be written as:

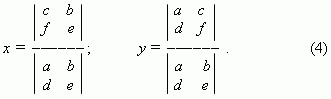
Formulas ( 4 ) are called Cramer’s rule for solution of the system of  two simultaneous linear equations in two unknowns.

E x a m p l e .  Solve the system of simultaneous equations

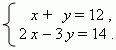
using Cramer’s rule.

S o l u t i o n . Here a = 1, b = 1, c = 12, d = 2, e = – 3, f = 14 .

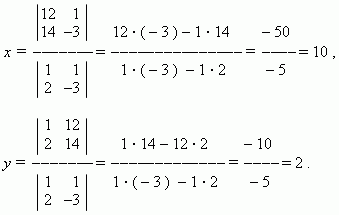
Investigation of solutions of a system of two simultaneous linear equations in two unknowns shows, that depending on coefficients three different cases are possible:

1) coefficients at unknowns in equations are disproportionate : a : d ≠ b : e ,

in this case the system of  simultaneous linear equations has a single solution ,

presented by formulas (4) ;

2) all coefficients of equations are proportional : a: d = b: e = c: f , in this case

the system of simultaneous linear equations has an infinite set of solutions ,

because we have actually one equation instead of two.

E x a m p l e . In the system

and this system has an infinite set of solutions. ( Why? )

Dividing the first equation by 2 and the second - by 3,

we’ll receive two identical equations:

that is one equation in two unknowns, which has an infinite set of solutions.

3) coefficients at unknowns are proportional, but disproportionate to free terms:

a : d = b : e ≠ c : f , in this case the system of simultaneous linear equations has

no solutions , because we have here contradictory equations.

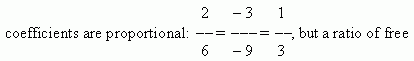terms is 7/12, not equal to 1/3. Why has not this system solution?

An answer is very easy. If to divide the second equation by 3,

we’ll receive:

These equations are contradictory, because the same expression

2 x – 3 y cannot be equal both to 7 and  4  simultaneously.