Systems of three simultaneous linear equations in three unknowns
Basic methods of solution. Substitution. Addition or subtraction
of equations. The third order determinants. Cramer's rule.
Systems of three simultaneous linear equations in three unknowns
have the shape:
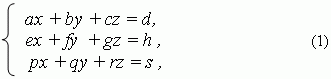
where a, b, c, d, e, f , g, h, p, q, r, s – numerical coefficients; x, y, z – unknowns. Solution of this system can be found by the same two basic methods, considered above: substitution and addition or subtraction. Here we’ll consider in details only Cramer’s method. At first, we’ll introduce the notion of the third order determinant.
The expression
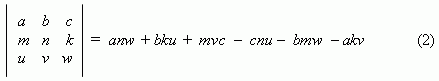
is called the third order determinant.
It isn’t necessary to remember this expression, because it is easy received, if to rewrite the table (2), repeating the two first columns on the right side. Then it is calculated by multiplication of numbers, located on the diagonals, going from
a, b, c
– to the right ( with the sign “ + ” ) and from
c, a, b
– to the left ( with the sign “ – ”), and summing these products:
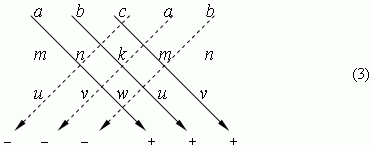
Using the third order determinant (2), the solution of (1) can be presented as:

These formulas are Cramer’s rule for solution of the system of three linear simultaneous equations in three unknowns.
E x a m p l e . Solve the following system of three simultaneous linear equations
by Cramer’s method:
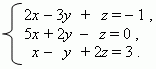
S o l u t i o n . Introduce the following notations: D – a denominator in the
formulas (4), Dx, Dy, Dz – numerators in the expressions
for x , y, z – correspondingly. Then, using the scheme (3),
we’ll receive:
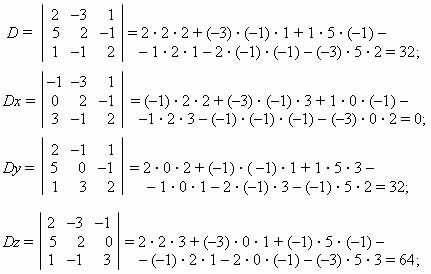
hence, by Cramer’s formulas ( 4 ) : x = Dx / D = 0 / 32 = 0;
y = Dy / D = 32 / 32 = 1; z = Dz / D = 64 / 32 = 2 .