Operations with negative and positive numbers
Subtraction. Multiplication. Division.
Rules of signs at multiplication and division.
Absolute value (modulus):
for a
negative number
this is a positive number, received by changing the sign " – " by " + "; for a
positive number and zero
this is the number itself. The designation of an absolute value (modulus) of a number is the two straight brackets insideof which the number is written.
E x a m p l e s :
| Addition: |
1) at addition of two numbers of the same sign their absolute values are added and before the sum their common sign is written.
E x a m p l e s : ( – 6 ) + ( – 5 ) = – 11 ; 2) at addition of two numbers with different signs their absolute values are subtracted(the smaller from the greater) and a sign of a number, having a greater absolute value is chosen. E x a m p l e s : ( – 6 ) + ( + 3 ) = – 3 . |
Subtraction:
it
is possible to change subtraction of two numbers by addition, thereat a minuend saves its sign, and a subtrahend is taken with the back sign.
E x a m p l e s :
( + 8 ) – ( – 5 ) = ( + 8 ) + ( + 5 ) = 13;
( – 8 ) – ( – 5 ) = ( – 8 ) + ( + 5 ) = – 3;
( – 8 ) – ( + 5 ) = ( – 8 ) + ( – 5 ) = – 13.
Multiplication:
at multiplication of two numbers their absolute values are multiplied, and a product has the sign " + ", if signs of factors are the same, and " – ", if the signs are different. The next scheme (
a rule of signs at multiplication
) is useful:
+ · – = –
– · + = –
– · – = +
At multiplication of some factors (two and more ) a product has the sign " + ", if a number of negative factors is even, and the sign " – ", if this number is odd.
E x a m p l e :
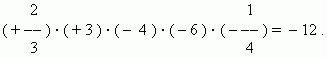
Division:
at division of two numbers the first absolutevalue is divided by the second and a quotient has the sign " + ", if signs of dividend and divisor are the same, and " – ", if they are different. The same rule of signs as at multiplication acts:
+ : – = –
– : + = –
– : – = +
E x a m p l e :