Complex numbers

The initial information about imaginary and complex numbers has been presented above, in the section “Imaginaryand complex numbers”. A necessity of these new kind numbers has appeared at solving of quadratic equations in the case of D < 0

( D – a discriminant of a quadratic equation). During a long time these numbers had no physical applications, therefore they were called “imaginary” numbers. But now these numbers have various applications in different physical and technical fields, such as: electrical engineering, hydro- and aerodynamics, theory of elasticity and others.

Complex numbers are written in the shape: a+ bi . Here a and b – real numbers , and i – an imaginary unit, i.e. i ² = –1. A real number a is called an abscissa of complex number a+ bi , and b – an ordinate of complex number a+ bi. Two

complex numbers a+ bi and a – bi are called the conjugate complex numbers.

Main agreements:

1.  A real number a can also be written in the shape of a complex number: a+ 0 i or a – 0 i . For example, the records  5 + 0 i and 5 – 0 i mean the same real number  5 .

2.  A complex number  0 + bi is called a pure imaginary number. The record bi means the same as  0 + bi .

3.  Two complex numbers a+ bi and c+ di are considered as equal ones, if a=c and b=d . Otherwise, the complex numbers aren’t equal.

Addition. A sum of complex numbers a+ bi and c+ di is called a complex number  ( a+ c ) + ( b+ d ) i. So, at addition of complex numbers their abscissas and ordinates are added separately. This definition corresponds to the rules of operations at usual polynomials.

Subtraction. A difference of two complex numbers a+ bi ( a minuend ) and c+ di ( a subtrahend )  is called a complex number  ( a – c ) + ( b – d ) i. So, at subtraction of two complex numbers their abscissas and ordinates are subtracted separately.

Multiplication. A product of complex numbers a+ bi and c+ di is called a complex number: ( ac – bd ) + ( ad + bc ) i.

This definition follows from two requirements:

1)  the numbers a+ bi and c+ di must be multiplied as algebraic bin omials,

2)  a number i has a main property: i ² = – 1.

E x a m p l e . ( a+ bi )( a – bi ) = a ² + b ² . Hence it follows, that

a product of two conjugate complex numbers  is a real positive number!

Division. To divide a complex number a+ bi ( a dividend ) by another c+ di ( a divisor ) means to find the third number e+ f i ( a quotient ), which being multiplied by the divisor c+ di ,  results the dividend a+ bi. If divisor isn’t equal to zero, then division is always valid.

E x a m p l e . Find  ( 8 + i ) : ( 2 – 3 i ) .

S o l u t i o n . Rewrite this quotient as a fraction:

Multiplying its numerator and denominator by  2 + 3 i and

executing  all operations, we’ll receive:

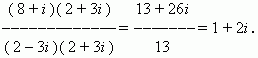
Geometric representationof complex numbers. Real numbers are represented by points in a numerical line:

Here a point A means a number –3, a point B – a number 2, and O – zero. In contrast this complex numbers are represented by points in a “numerical” ( coordinate )  plane. For this we select a system of rectangular  ( Cartesian ) coordinates with the same scale in both axes. Then, a complex number a+ bi will be represented by point P with abscissa a and ordinate b ( see figure ). This coordinate system is called a complex plane .

___

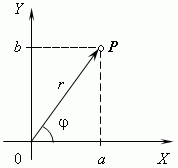
Modulus of a complex number is a length of vector OP , representing this complex number in a coordinate( complex ) plane. Modulus of complex number a+ bi is signed as  | a+ bi |  or  by letter r and equal to :

Conjugate complex numbers havethe same modulus.

___

Argument of a complex number is the angle between x -axis and vector OP , representing this complex number.

Trigonometric form of a complex number. Abscissa a and ordinate b of the complex number a + bi can be expressed by its modulus r and argument :

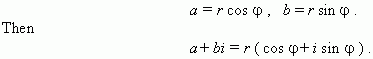
Operations with complex numbers, represented in the trigonometric form.

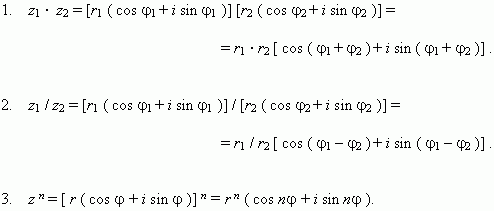
This is the famous Moivre’s  formula.

Here k is any integer. To receive n different values of the n -th degree root of z it’s necessary to give n consecutive values for k ( e.g., k = 0, 1, 2,…, n – 1) .