Proving and solving of inequalities
Equivalent inequalities. Method of intervals. Double inequality.
Systems of simultaneous inequalities.
Proving of inequalities. There are some ways to prove inequalities. We’ll consider them to prove the inequality:
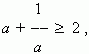 where
a –
a positive number .
where
a –
a positive number .
1).
Using of the known or before proved inequality.
It is known, that: (
a
– 1
)
²
![]() 0 .
0 .
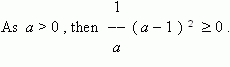 Opening the brackets, we’ll receive:
Opening the brackets, we’ll receive:
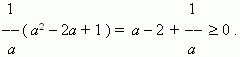
Hence it follows:
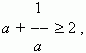 which was to be proved
.
which was to be proved
.
2).
Estimating of the sign of difference between sides of inequality
. Consider the
difference between the left and the right sides:
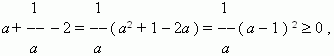
moreover, the equality takes place only if a = 1 .
3). Reductio ad absurdum proof ( an indirect proof ) . Assume the contrary proposition:
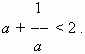
Multiplying both of the sides by
a
, we’ll receive:
a
²
+
1 < 2
a
,
i.e.
a
²
+ 1 – 2
a
< 0 , or
(
a
– 1
)
²
< 0,
that is wrong. ( Why ? ) .
The received contradiction proves the validity of the considered inequality.
4).
Using of an indefinite inequality.
An
indefinite inequality
is an inequality with the sign \/ or /\ , when we don’t know how
to turn this sign to receive the valid inequality. There are the same rules of operations as
for inequalities, containing the signs > or < .Consider the indefinite inequality:
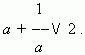
Multiplying both of the sides by
a
, we receive:
a
²
+ 1\/ 2
a
, i.e.
a
²
+ 1 – 2
a
\/ 0 , or
(
a
– 1 )
²
\/
0 ,
but here we know, how to turn the sign \/ to receive the valid inequality.
( How ? ). Turning it in the whole chain of transformations to the right direction, we
receive the inequality, which was to be proved.
Solving of inequalities. Two inequalities, containing the same unknowns, are called equivalent , if they are valid at the same values of the unknowns . The same definition is used for the equivalence of two systems of simultaneous inequalities. Solving of inequalities is a process of transition from one inequality to another, equivalent inequality. For this purpose main properties of inequalities are used (see above). Besides this, an exchange of any expression by another, identical one may be used. Inequalities can be algebraic (containing only polynomials) and transcendental (for instance, logarithmic or trigonometric inequalities). We’ll consider here one very important method, often used at solving algebraic inequalities.
Method of intervals. Solve the inequality: ( x – 3 )( x – 5 ) < 2( x – 3 ) . It’s impossible to divide both of the sides of this inequality by ( x – 3 ), because we don’t know the sign of this binomial (it contains unknown x ). So, we must transfer all terms to the left-hand side:
and after factoring the left-hand side expression is following:
we receive: ( x – 3 )( x – 7 ) < 0. Now we determine the sign of the left side product in different numerical intervals. Note, that x = 3 and x = 7 are the roots of this expression. Therefore, the whole numerical line is divided by these roots to the following three intervals:
In the interval
I
(
x
< 3
) both factors are negative, so their
product is positive
; in the interval
II
( 3 <
x
< 7 ) the first factor (
x
– 3 ) is positive, and the second factor (
x –
7 ) is negative, so their
product is negative
; in the interval
III
(
x
> 7 ) both of the factors are positive, so their
product is also positive.
Now we must select the
interval within which
our
product is
negative.
This is the interval
II
, hence we have the solution: 3 <
x
< 7.
The last expression is the so called a
double inequality
. It means that
x
must be greater than 3 and less than 7 simultaneously.
E x a m p l e . Solve the following inequality by the method of intervals:
S o l u t i o n . The roots of the left-hand side of this inequality are: 1, 2, 3, …, 100.
The numerical line will be divided by these roots into 101 intervals:
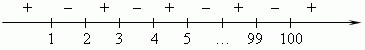
Note, that number of the factors from the left is equal to 100, i.e. an
even
number. Hence, at
x
< 1 all factors are negative and theirproduct is
positive
.
Then we’ll have a change of the product sign at transition of any next root.
Therefore, the next interval, within which the product is positive will be
( 2, 3 ) , then ( 4, 5 ) , then ( 6, 7 ) , … , ( 98, 99 ) and the last interval is
x
>100. So, the given inequality has the solution:
x
< 1, 2 <
x
< 3, 4 <
x
< 5 ,…,
x
>100.
Thus,
to solve some algebraic inequality it’s necessary to transfer all terms to the left (or to the right) side of the inequality and to solve the corresponding equation. After this, the numerical line is divided by the found roots into some intervals. In the last stage of solution it is necessary to determine the sign of the polynomial within each of these intervals and to select the necessary intervals according to the sense of your inequality.
Note that the most of transcendental inequalities are reduced by exchange of unknown to an algebraic inequality. Then it should be solved in new unknowns; after the inverse exchange of unknown it is solved finally in the given unknowns.
Systems of simultaneous inequalities. To solve the system of simultaneous inequalities it is necessary to solve each of them and to compare their solutions. This comparison results to one of two possible cases: either the system has a solution as a whole or does not.
E x a m p l e 1. Solve the system of simultaneous inequalities:
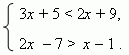
S o l u t i o n. The first inequality solution: x < 4 ; and the second: x > 6. Thus, this system of
simultaneous inequalities has no solution. ( Why ? )
E x a m p l e 2. Solve the system of simultaneous inequalities:
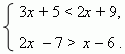
S o l u t i o n. The first inequality as before gives:
x
< 4; but the second inequality gives in this
case:
x
> 1. Thus, there is the solution: 1 <
x
< 4.