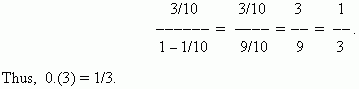Arithmetic and geometric progressions
Arithmetic progression. Geometric progression. Infinitely decreasing
geometric progression. Converting of repeating decimal to vulgar fraction.
Sequences.
Let’s consider the series of natural numbers: 1, 2, 3, … ,
n
– 1,
n
, … .
If to replace each natural number
n
in this series by some number
u
n
, subordinated to some law, we’ll receive a new series of numbers:
called a
numerical sequence
. A number
u
n
is called a
general term
of the numerical sequence.
E x a m p l e s of numerical sequences:
Arithmetic progression. The numerical sequence, in which each next term beginning from the second is equal to the previous term, added with the constant for this sequence number d , is called an arithmetic progression . The number d is called a common difference. Any term of an arithmetic progression is calculated by the formula:
A sum of n first terms of arithmetic progression is calculated as:
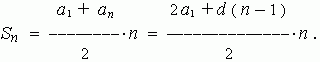
E x a m p l e . Find a sum of the first 100 odd numbers.
S o l u t i o n . Use the last formula. Here
a
1
= 1,
d
= 2
.
So, we have:
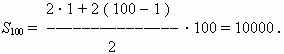
Geometric progression. The numerical sequence, in which each next term beginning from the second is equal to the previous term, multiplied by the constant for this sequence number q , is called a geometric progression . The number q is called a common ratio. Any term of a geometric progression is calculated by the formula:
A sum of n first terms of geometric progression is calculated as:
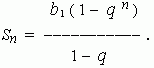
Infinitely decreasing geometric progression.
This is the geometric progression, with
|
q
| < 1 . For it the notion of a
sum of infinitely decreasing geometric progression
is determined as a number, to which a sum of the first
n
terms of the considered progression unboundedly approximates at an unbounded increasing of number
n
. The infinitely decreasing geometric progression sum is calculated by the formula:
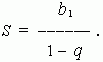
E x a m p l e . Find the sum of the infinitely decreasing geometric progression:
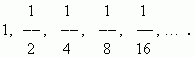
S o l u t i o n . Use the last formula. Here b 1 = 1, q = 1/2. So, we have:
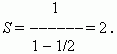
Converting of a repeating decimal to a vulgar fraction. Assume, that we want to convert the repeating decimal 0.(3) to a vulgar fraction. Consider this decimal in the more natural form:
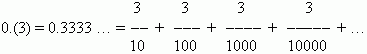
This is the infinitely decreasing geometric progression with the first term 3/10 and a common ratio q = 1/10. According to the above shown formula the last sum is equal to: