Logarithms
logarithms. Common logarithm. Natural logarithm.
A
logarithm
of a positive number N to the base
b
(
b
>
0,
b
1
)
is called
an exponent of a power
x
, to which
b
must be raised to receive N
.
The designation:
&
nbsp; &n
bsp;
This record is identical to the following one:
E x a m p l e s :
The above presented definition of logarithm may be written as the logarithmic identity :
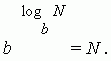
The main properties of logarithms.
1) log b = 1 , because b 1 = b .
b & nbsp;
& nbsp;
2) log 1 = 0 , because b 0 = 1 .
b
3) Logarithm of a product is equal to a sum of logarithms of factors:
log ( ab ) = log a + log b .
4) Logarithm of a quotient is equal to a difference of logarithms of dividend and divisor:
log ( a / b ) = log a – log b .
5) Logarithm of a power is equal to a product of an exponent of the power by logarithm of its base:
A consequence of this property is the following: logarithm of a root is equal to the logarithm of radicand divided by the degree of the root:
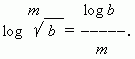
6) If a base of logarithm is a power, then a value, reciprocal to this power exponent, may be carried out of the logarithm symbol:
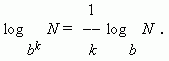
The two last properties may be united in the general property:
& nbsp;
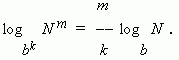
7) The transition module formula ( i.e. a transition from one base of the logarithm to another base ):
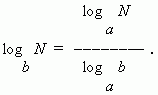
& nbsp; &n bsp; &nb sp; &nbs p;
In the particular case: N = a we have:
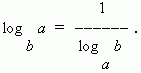
Common logarithm is a logarithm to the base 10. It marks as lg , i.e. log 10 N = lg N . Logarithms of the numbers 10, 100, 1000, ... are equal to 1, 2, 3, … correspondingly, i.e. they have as many positive ones as many zeros are placed in the number after one. Logarithms of the numbers 0.1, 0.01, 0.001, ... are equal to –1, –2, –3, …, i.e. they have as many negative ones as many zeros are placed in the number before one ( including zero of integer part ). Logarithms of the rest of the numbers have a fractional part, called a mantissa . An integer part of logarithm is called a characteristics . Common logarithms are the most suitable for practical use.
Natural logarithm is a logarithm to the base å . It marks as ln , i.e. log e N = ln N . The number å is irrational, its approximate value is 2.718281828459045. This number is a limit, which the number ( 1 + 1 / n ) n approaches at unbounded increasing of n ( see the first remarkable limit on the page "Sequences. Limits of numerical sequences. Some remarkable limits" ). Strange though it may seem, natural logarithms are very suitable at different operations in analysis of functions. Calculation of logarithms to the base å is executed quicker, than to any other base .