Theory of combinations. Newton’s binomial
Binomial coefficients. Pascal's triangle. Properties of binomial coefficients.
By the general name “combinations” we call three kinds of combinations, composed from some number of different elements, belonging to the same set ( for instance, letters of an alphabet, books of a library, cars on a parking, etc.).
Permutations. Take n different elements a
1 , a 2 , a 3 , …, a n . We’ll permute them in all possible ways, saving their quantity and changing only their order. Each of combinations, received so, is called a permutation. A total quantity of permutations of n elements is signed as P n .This number is equal to a product of all integer numbers from 1 to n :
The symbol n ! ( it is called a factorial ) is an abridged record of the product 1 · 2 · 3 · … · ( n – 1 ) · n .
E x a m p l e . Find a number of permutations of three elements a , b , c .
S o l u t i o n . According to the above presented formula:
P
3
= 1 · 2 · 3 = 6.
Actually, we
have 6 permutations:
abc, acb, bac, bca, cab, cba.
Arrangements. Compose groups of m different elements, taken from a set of n elements, placing these m taken elements in a different order. The received combinations are called arrangements of n elements taken m at a time.
Their total quantity
is signed as:
and equal to the product:
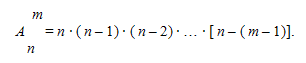
E x a m p l e . Find a number of arrangements of four elements a, b, c, d taken two at a time.
S o l u t i o n .According to this formula we have:
These arrangements are: ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc.
Combinations. Compose groups of m different elements, taken from a set of n elements, not taking into consideration an order of these m taken elements. So, we received combinations of n elements taken m at a time.
Their total quantity is signed as
and can be calculated
by the formula:
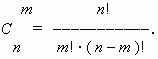
From this formula it is clear, that
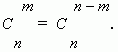
Note, that it is possible to compose
only
one combination of
n
elements taken
n
at a time,
that
contains
all
n
elements. T
he above shown formula gives this value only if to assume,
that
0! = 1.
This is the definition of 0!
.
According to this we have now:
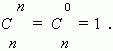
Also another expression is used for total quantity of combinations:
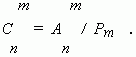
E
x a m p l e . Find a number of all combinations of five elements:
a, b, c, d, e
taken
three at a time.
S o l u t i o n :
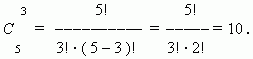
All these combinations are: abc, abd, abe, acd, ace, ade, bcd, bde, cde.
Newton’s binomial. This is the formula, representing the expression (
a + b ) n at positive integer n as the polynomial:
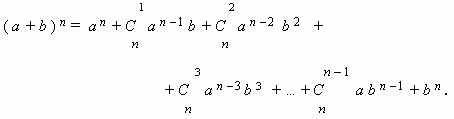
Note, that a sum of exponents of powers for a and b is the constant, equal to n.
E x a m p l e 1 .
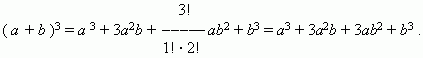
( See above one of the formulas of abridged multiplication).
Numbers
are called
binomial coefficients.
They can be received only by an addition, using the following scheme. In the upper row we write two units. All following rows begin and end with 1. Intermediate numbers in these rows are received as a sum of neighboring numbers from the previous row. This scheme is called Pascal’s triangle :
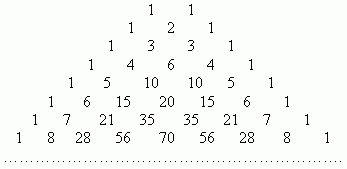
The first row in this table contains binomial coefficients for n = 1; the second row - for n = 2; the third row - for n = 3 and so on.Therefore, if it is necessary, for instance, to expand an expression:
we can receive the result at once, using the table:
Properties of binomial coefficients.
1. A sum of coefficients of an expansion ( a + b ) n is equal to 2
n .To prove this, it’s sufficient to assume a = b = 1. Then, in the right side in Newton’s binomial we’ll have a sum of coefficients :
2.
Coefficients of terms, equally removed from ends of the expansion, are equal.
This property follows from the relation:
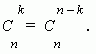
3. A sum of coefficients of even term is equal to a sum of coefficients of odd terms, and each of them is equal to
To prove this property we’ll use the binomial:
Here even terms have the sign " + ",
odd terms - the sign " - ". As the expansion result is 0, hence, sums of
their binomial coefficients are equal one to another, therefore each of them is equal to:
which was to be proved.