Division of polynomials
Division of polynomials. What means to divide one polynomial P by another Q ? It means to find polynomials M ( quotient ) and N ( remainder ), satisfying the two requirements:
1). An equality
MQ + N = P
takes place;
2). A degree of polynomial
N
is less than a degree of polynomial
Q
.
Division of polynomials can be done by the following scheme (
long division
):
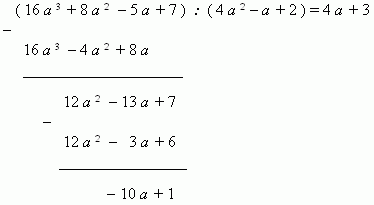
1) Divide the first term 16
a
3
of the dividend by the first term 4
a
2
of the divisor; the result
4
a
is the first term of the quotient.
2) Multiply the received term 4
a
by the divisor 4
a
2
– a +
2; write the result 16
a
3
–
4
a
2
+
8
a
under the dividend, one similar term under another.
3) Subtract terms of the result from the corresponding terms of the dividend and move down the next by the order term 7 of the dividend; the remainder is 12
a
2
–
13
a +
7 .
4) Divide the first term 12
a
2
of this expression by the first term 4
a
2
of the divisor; the result 3 is the second
term of the quotient.
5) Multiply the received second term 3 by the divisor 4
a
2
– a +
2; write the result
12
a
2
–
3
a +
6 again under the dividend, one similar term under another.
6) Subtract terms of the result from the corresponding terms of the previous remainder
and receive the second remainder:
–
10
a
+
1. Its degree is less than the divisor degree, therefore the division has been finished. The quotient is 4
a +
3,
the remainder is
–
10
a +
1.