Definite integral. Newton – Leibniz formula
Definite integral. Limits of integration. Integrand.
Newton-Leibniz formula.
Consider a continuous function y = f ( x ), given on a segment [ a , b ] and saving its sign on this segment ( Fig.8 ). The figure, bounded by a graph of this function, a segment [ a , b ] and straight lines x = a and x = b , is called a curvilinear trapezoid . To calculate areas of curvilinear trapezoids the following theorem is used:
If f – a continuous, non-negative function on a segment [
a , b ], and F – its primitive on this segment, then an area S of the corresponding curvilinear trapezoid is equal to an increment of the primitive on a segment [ a, b ], i.e.
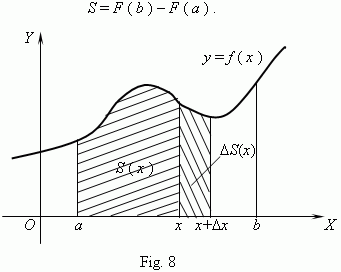
Consider a function
S
(
x
), given on a segment [
a
,
b
]. If
a
<
x
b
, then
S
(
x
) is an area of the part of the curvilinear trapezoid, which is placed on the left of a vertical straight line, going through the point (
x
, 0 ). Note, that if
x
=
a
, then
S
(
a
) = 0 and
S
(
b
) =
S
(
S –
area of the
curvilinear trapezoid
). It is possible to prove, that
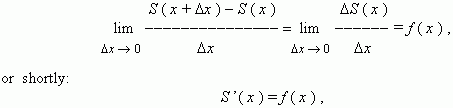
i.e.
S
(
x
) is a primitive for
f
(
x
). Hence, according to the basic property of primitives, for all
x
[
a
,
b
] we have:
where
C
– some constant,
F
– one of the primitives for a function
f .
To find
C
we substitute
x
=
a :
hence, C = - F ( a ) and S ( x ) = F ( x ) - F ( a ). As an area of the curvilinear trapezoid is equal to S ( b ) , substituting x = b , we’ll receive:
E x a m p l e . Find an area of a figure, bounded by the curve
y
=
x
2
and lines
y
= 0,
x
= 1,
x
= 2 ( Fig.9 ) .
Definite integral. Consider another way to calculate an area of a curvilinear trapezoid. Divide a segment [ a , b ] into n segments of an equal length by points:
and let
= (
b
–
a
) /
n
=
x
k
-
x
k
-
1
, where
k
= 1, 2, …,
n –
1,
n .
In each of segments [
x
k
-
1
,
x
k
] as on a base we’ll build a rectangle of height
f
(
x
k
-
1
)
.
An area of this rectangle is equal to:
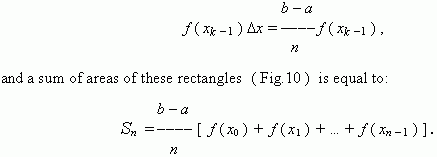
In view of continuity of a function
f
(
x
) a union of the built rectangles at great
n
(i.e. at small
) "almost coincides" with our curvilinear trapezoid. Therefore,
S
n
S
at great values of
n
. It means, that
This limit is called
an
integral
of a function
f
(
x
)
from
a
to
b
or a
definite integral
:
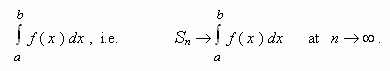
Numbers
a
and
b
are called
limits of integration
,
f
(
x
)
dx
– an
integrand
.
So, if
f
(
x
)
0 on a segment [
a
,
b
] , then an area
S
of the corresponding
curvilinear trapezoid is represented by the formula:
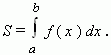
Newton – Leibniz formula. Comparing the two formulas of the curvilinear trapezoid area, we make the conclusion: if F ( x ) is primitive for the function f ( x ) on a segment [ a , b ] , then
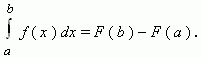
This is the famous Newton – Leibniz formula. It is valid for any function f ( x ), which is continuous on a segment [ a , b ] .
S o l u t i o n. Using the table of integrals for some elementary functions ( see above ), we’ll receive:
