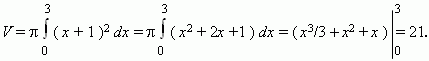Geometrical and mechanical applications of definite integral

A definite integral has numerous applications in mathematics, mechanics, physics, astronomy, engineering and other fields of human activities. We’ll consider here only two examples, illustrating possibilities of this apparatus.

A volume of revolution body. Consider a body, received by revolution around an axis OX of a curvilinear trapezoid, bounded by the function f ( x )  graph,straight lines x = a and x = b and an axis OX ( Fig.10).

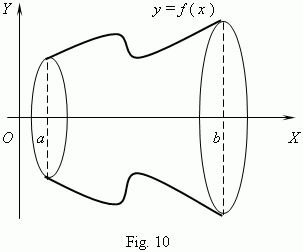
A volume V of the revolution body is:

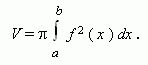
A work of variable force. Consider motion of a material point, moving along an axis OX under the influence of variable force f , depending on the point position x on the axis, i.e. the force is a function of x .  Then a work A , necessary to move the material point from the position x = a to the position x = b is calculated by the formula:

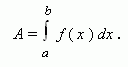
E x a m p l e .  Find a volume of a truncated cone, formed by revolution of the straight line
y = x + 1 around an axis OX and bounded by lines x = 0  and x = 3 .

S o l u t i o n .  According to the above represented formula we have: