Limits of functions
Infinitesimal and infinite values. Finite limit.
Infinite limit. Notion of an infinity.
Limit of a function.
A number
L is called a limit of a function y = f
(
x
)
as x tends a :
if and only if for any
> 0
one can find such a positive number
=
(
),
depending on
,
that
|
x
–
a
| <
implies that
|
f
(
x
) –
L
| <
.
This definition means, that
L
is a
limit
of a function
y
=
f
(
x
) , if the function value approaches unrestrictedly to
L
, when the argument value
x
approaches
a
. Geometrically it means, that for any
> 0 it is possible to find such a number
, that if
x
is within an interval (
a
–
,
a
+
), then a function value is within an interval (
L
–
,
L
+
). Note, that according to this definition, a function argument
x
only
approaches
a
, not adopting this value! It must be considered at calculating limit of any function at a point of its discontinuity ( i.e., where this function doesn’t exist ).
E x a m p l e . Find :
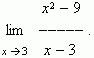
S o l u t i o n . Substituting
x
= 3 into the expression
we’ll receive a meaningless
expression
( see
"About meaningless expressions"
in the section "Powers and roots"
of the part "Algebra"). Therefore we’ll solve in a different way:
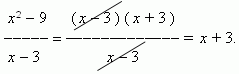
Here the fraction canceling is valid, because
x
3 , it only
approaches
3.
Now we have:
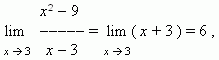
because, if x approaches 3 , then x + 3 approaches 6 .
Some remarkable limits.
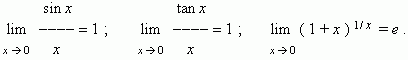
Infinitesimal and infinite value. If limit of some variable is equal to 0, this variable is called an infinitesimal .
E x a m p l e . The function
y
=
is an infinitesimal, if
x
approaches 4, because
If an absolute value of some variable increases unboundedly, then this variable is called an infinite value .
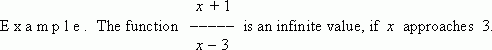
An infinite value has no a finite limit, but it has so called an infinite limit; this fact is written as:
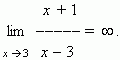
The symbol
("infinity") doesn’t mean some number, it means only that the fraction increases unboundedly if
x
approaches 3. It should be noted, that the fraction can be both positive (at
x
> 3) and negative (at
x
< 3). If an infinite value can be only positive at any values of
x
, it is marked in a record. For example, at
x
0 the function
y
=
x
–2
is an infinite value, but it is positive both at
x
> 0 and at
x
< 0 ; this is expressed as:
On the contrary, the function y = – x –2 is always negative, therefore
According to this, a result of our example can be written as:
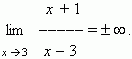
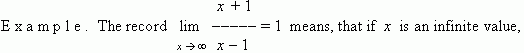
then this fraction approaches 1 , i.e. its limit is 1.