Derivative. Geometrical and mechanical meaning of derivative
Geometrical meaning of derivative. Slope of a tangent. Tangent equation.
Mechanical meaning of derivative. Instantaneous velocity. Acceleration.
Derivative.
Consider a function
y
=
f
(
x
) at two points:
x
0
and
x
0
+
:
f
(
x
0
) and
f
(
x
0
+
). Here
means some small change of an argument, called an
argument increment
; correspondingly a difference between the two values of a function:
f
(
x
0
+
) –
f
(
x
0
) is called a
function increment
.
Derivative
of a function
y
=
f
(
x
) at a point
x
0
is the limit:
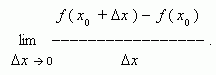
If this limit exists, then a function f ( x ) is a differentiable function at a point x 0 . Derivative of a function f ( x ) is marked as:
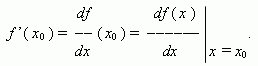
Geometrical meaning of derivative.
Consider a graph of a function
y
=
f
(
x
) :
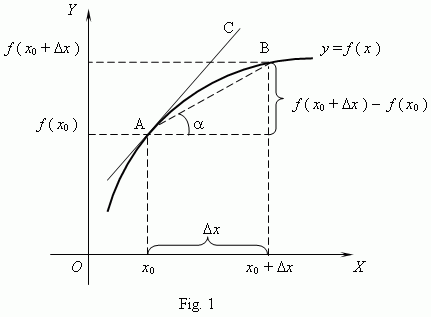
From Fig.1 we see, that for any two points A and B of the function graph:
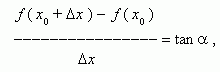
where
- a slope angle of the secant AB.
So, the difference quotient is equal to a secant slope. If to fix the point A and to move the point B towards A, then
will unboundedly decrease and approach 0, and the secant AB will approach the tangent AC. Hence, a limit of the difference quotient is equal to a slope of a tangent at point A. Hence it follows:
a derivative of a function at a point is a slope of a tangent of this function graph at this point.
Tangent equation.
Now we’ll derive an equation of a tangent of a function graph at a point
A
(
x
0
,
f
(
x
0
)). In general case an equation of a straight line with a slope
f
’(
x
0
) has the shape:
To find
b
we’ll
use the fact, that a tangent line goes through a point A :
hence,
b
=
f
(
x
0
) –
f
’(
x
0
)
·
x
0
, and substituting this expression instead of
b
, we’ll receive the equation of a tangent:
Mechanical meaning of derivative.
Consider the simplest case: a movement of a material point along a coordinate line, moreover, the motion law is given, i.e. a coordinate
x
of this moving point is the known function
x
(
t
)
of time
t
. During the time interval from
t
0
till
t
0
+
the point displacement is equal to:
x
(
t
0
+
) –
x
(
t
0
) =
, and its
average velocity
is:
v
a
=
/
.
As
0, then an average velocity value approaches the certain value, which is called an
instantaneous velocity v
(
t
0
) of a material point in the moment
t
0
. But according to the derivative definition we have:
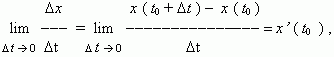
hence, v ( t 0 ) = x’ ( t 0 ), i.e. a derivative of a coordinate with respect to time is a velocity. This is a mechanical meaning of a derivative. Analogously to this, an acceleration is a derivative of a velocity with respect to time : a = v’ ( t ).