Convexity, concavity and inflexion points of a function
Sufficient condition of concavity ( convexity ) of a function.
Inflexion point.
The second derivative.
If a derivative
f '
(
x
) of a function
f
(
x
) is differentiable
in the point (
x
0
), then its derivative is called the second derivative of the function
f
(
x
) in the point (
x
0
) and denoted as
f ''
(
x
0
).
A function
f
(
x
) is called
convex
in an interval (
a
,
b
), if the function
f
(
x
) graph
is placed in this interval
lower
than a tangent line, going through any point (
x
0
,
f
(
x
0
) ),
x
0
(
a
,
b
).
A function
f
(
x
) is called
concave
in an interval (
a
,
b
), if the function
f
(
x
) graph
is placed in this interval
higher
than a tangent line, going through any point (
x
0
,
f
(
x
0
) ),
x
0
(
a
,
b
).
Sufficient condition of concavity (convexity) of a function.
Let a function
f
(
x
) be twice differentiable (i.e. it has the
second
derivative) in an interval (
a
,
b
), then:
if
f ''
(
x
) > 0 for any
x
(
a
,
b
),
then the function
f
(
x
) is
concave
in the interval (
a
,
b
); if
f ''
(
x
) < 0 for any
x
(
a
,
b
), then the function
f
(
x
)
is
convex
in the interval (
a
,
b
).
If a function changes a convexity to a concavity or vice versa at passage through some point, then this point is called an inflexion point an inflexion point. Hence it follows, that if the second derivative f '' exists in an inflexion point x 0 , then f '' ( x 0 ) = 0.
| E x a m p l e. |
Consider a graph of the function
y
=
x
3
:
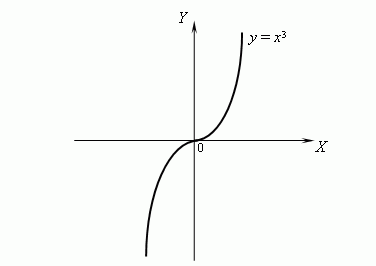
This function is concave at x > 0 and convex at x < 0. In fact, y'' = 6 x , but 6 x > 0 at x < 0 and 6 x < 0 at x < 0, hence, y'' > 0 at x 3 0 and y'' < 0 at x < 0, hence it follows, that the function y = x 3 is concave at x > 0 and convex at x < 0. Then the point x = 0 is the inflexion point of the function y = x 3 . |