Integration methods
Integration by parts.
If functions
u
(
x
) and
v
(
x
) have continuous first derivatives
and the integral
v
(
x
)
du
(
x
) exists, then the integral
u
(
x
)
dv
(
x
) also exists and the equality
u
(
x
)
dv
(
x
) =
u
(
x
)
v
(
x
)
du
(
x
)
takes place, or shortly:
u dv
=
u v
–
v du
.
Pay attention to the fact, that this operation and a differential of product of two functions are mutually inverse operations ( check, please ! ).
| E x a m p l e. |
Find the integral:
ln
x dx
.
|
| S o l u t i o n. |
If to suppose that
u
= ln
x
and
dv
=
dx
, then
du
=
dx
/
x
and
v
=
x
. Using the formula of integration by parts, we receive:
|
Integration by substitution (exchange).
If a function
f
(
z
) is given and has a primitive at
z
Z
, a function
z
=
g
(
x
) has a continuous derivative at
x
X
, and
g
(
X
)
Z
, then the function
F
(
x
) =
f
[
g
(
x
)]
F
(
x
)
dx
=
f
[
g
(
x
)]
f
(
z
)
dz
.
| E x a m p l e. |
Find the integral:
.
|
| S o l u t i o n. |
To get rid of the square root we assume
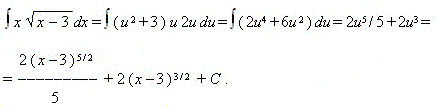
, then
x = u
2
+ 3
and hence,
dx =
2
u du
. Then exchanging, we have:
|