De L'Hospital’s rule
Let at
x
a
for
functions
f
(
x
) and
g
(
x
),
differentiable
in some neighborhood
of the point
a
, the conditions are executed:
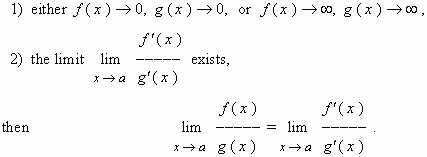
This theorem is called
de L'Hospital’s rule
. It allows to calculate limits of ratios of
functions, when both a numerator and a denominator approach either zero, or infinity. As mathematicians say,
de
L'Hospital’s rule
permits to get rid of indeterminacies of types
0 / 0 and
/
.
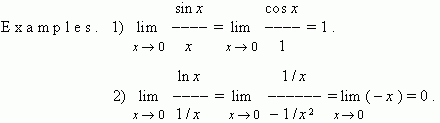
At indeterminacies of other types:
–
,
×
0
, 0
0
,
0
,
it is necessary to do some
identical
transformations to reduce them to
one of these two indeterminacies:
either 0 / 0 , or
/
.
After this it is possible to use de L'Hospital’s rule. Show some of possible transformations of the above
mentioned indeterminacies.
| 1) |
–
:
let f ( x )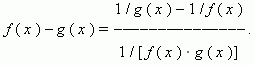
,
g
(
x
)
, then this indeterminacy is reduced to the type 0 / 0 by the following transformation:
|
| 2) |
|
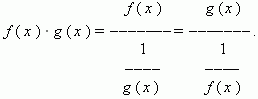
| 3) |
the rest of the indeterminacies are reduced to the first ones by the logarithmic
transformation:
|
If after using of de L'Hospital’s rule the indeterminacies of the types 0 / 0 or
/
remain, it is necessary to repeat it. The multifold use of de L'Hospital’s rule can
give the required result. The de L'Hospital’s rule is also applicable, if
x
.