Transformations of coordinates
Translation of axes. Turning around origin of coordinates.
Central symmetry. Homothetic transformation. Affine transformation.
Consider some transformations tied with a transition from one coordinate system to another. Here ( õ , ó ) è ( õ ' , ó ' ) are coordinates of arbitrary point P in old and new coordinate systems correspondingly.
Translation of axes. Let's move the coordinate system XOY in a plane so, that the axes OX and OY are parallel to themselves, and the origin of coordinates Î moves to the point Î ' ( a , b ). We'll receive the new coordinate system X'O'Y' ( Fig.1 ):
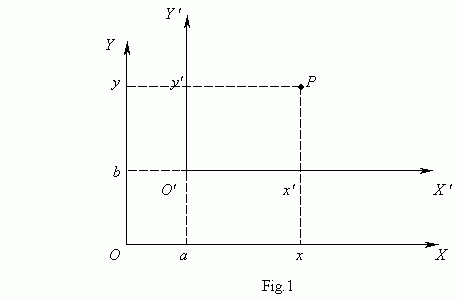
Coordinates of the point P in the new and old coordinate systems are tied by the equations:
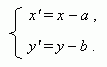
Turning around origin of
coordinates.
Let's
turn the coordinate system
X
Î
Y
in
a
plane by an angle
(
Fig.2
).
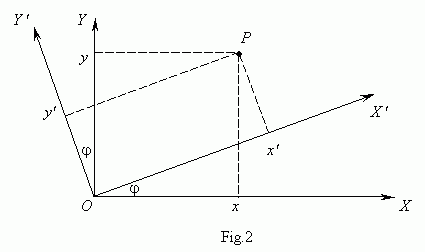
Now coordinates of the point P in the new and old coordinate systems are tied by the equations:
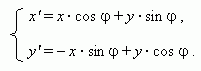
In the particular case:
=
we'll receive
a
central symmetry
relatively the origin
of
coordinates
O
:
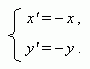
A
homothetic transformation
with a center
O
(
a
,
b
)
and a
coefficient
k
0 :
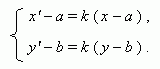
An affine transformation:
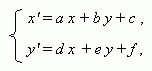
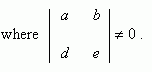
An affine transformation transfers straight lines to straight lines, intersecting lines to intersecting lines, parallel straight lines to parallel straight lines. All above mentioned transformations of coordinates are affine transformations.