Circle

Circle. Center of circle. Radius of circle.

Equation of circle. Equation of tangent line to circle.

Tangency condition of straight line and circle.

A circle ( Fig.1 ) is a locus of points, equidistant from the given point Î , called a center of circle , at the distance R . A number R > 0 is called a radius of circle .

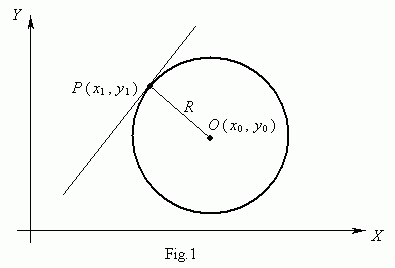
An equation of circle of radius R with a center in a point Î ( õ ₀ , ó ₀ ) is:

( õ – õ ₀ ) ² + ( ó – ó ₀ ) ² = R ² .

If a center of the circle coincides with the origin of coordinates , then an equation of circle becomes :

õ ² + ó ² = R ² .

Let Ð ( õ ₁ , ó ₁ ) be a point of the circle ( Fig.1 ), then an equation of tangent line to circle in the given point is:

( õ ₁ – õ ₀ ) ( õ – õ ₀ ) + ( ó ₁ – ó ₀ ) ( ó – ó ₀ ) = R ² .

A tangency condition of a straight line y = m x + k and a circle õ ² + ó ² = R ² :

k ² / ( 1 + m ² ) = R ² .

Back