Hyperbola
Hyperbola . Focuses . Equation of hyperbola. Focal length.
Real and imaginary axes of hyperbola. Eccentricity.
Asymptotes of hyperbola. Equation of tangent line to hyperbola.
Tangency condition of straight line and hyperbola.
A hyperbola ( Fig.1 ) is called a locus of points, a modulus of difference of distances from which to the two given points F 1 and F 2 , called focuses of hyperbola, is a constant value.
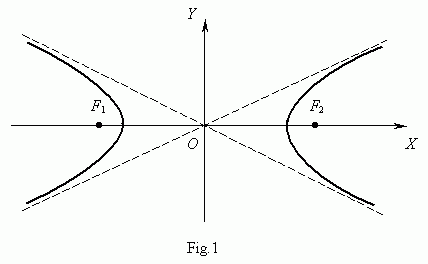
An equation of hyperbola ( Fig.1 ) is :
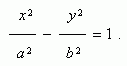
Here the origin of coordinates is a center of symmetry of hyperbola, and the coordinate axes are its axes of symmetry.
The segment
F
1
F
2
= 2
ñ
,
where
is
called
a focal length
.
The segment
AB
= 2
a
is called
a real axis
of hyperbola, the segment
CD
= 2
b
is called
an imaginary
axis
of hyperbola. The number
e
=
c
/
a
,
e
> 1 is called
an
eccentricity
of
hyperbola. The straight lines
y
=
±
(
b
/
a
)
x
are
called
asymptotes of hyperbola
.
Let Ð ( õ 1 , ó 1 ) be a point of hyperbola, then an equation of tangent line to hyperbola in this point is:
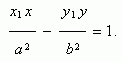
A tangency condition of a straight line y = m x + k and a hyperbola õ 2 / a 2 – ó 2 / b 2 = 1 :
k 2 = m 2 a 2 – b 2 .