Transformations of coordinates
Translation of axes. Homothetic transformation.
Symmetry. Affine transformation.
Consider some transformations tied with a transition from one coordinate system to another. Here ( õ , ó , z ) and ( õ ' , ó ' , z ' ) are coordinates of arbitrary point P in old and new coordinate systems correspondingly.
Translation of axes. Let's move the coordinate system XYZ in a space so, that axes OX , OY and OZ are parallel to themselves, and the origin of coordinates Î moves to the point Î ' ( a , b , ñ ). We'll receive a new coordinate system X'Y'Z' . Coordinates of the point P in the new and old coordinate systems are tied by the equations:
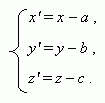
A
homothetic transformation
with a center
O
(
a
,
b
,
c
)
and
a coefficient
k
![]() 0 :
0 :
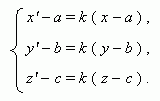
A symmetry relatively the plane XOY :
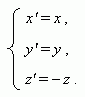
An affine transformation:
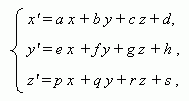

An affine transformation transfers straight lines to straight lines, intersecting lines to intersecting lines, crossing straight lines to crossing straight lines, parallel straight lines to parallel straight lines. All above mentioned transformations of coordinates are affine transformations.