Functional dependence between two variables
Function. Single-valued function. Multiple-valued function.
Two variables x and y are tied by a functional dependence , if for each value of one of them it is possible to receive by the certain rule one or some values of another.
| E x a m p l e . |
A temperature
T
of water boiling and atmosphere pressure
p
are tied by
a functional dependence,
because each value of pressure corresponds to a certain value of the temperature and inversely. So, if p = 1 bar, then T = 100°C; if p = 0.5 bar, then T = 81.6°C. |
A variable, values of which are given, is called an argument or an independent variable; the other variable, values of which are found by the certain rule is called a function. Usually an argument is marked as x , and a function is marked as y . If only one value of function corresponds to each value of argument, this function is called a single-valued function ; otherwise, if there are many corresponding values, this function is called a multiple-valued function ( two-valued, three-valued and etc.).
| E x a m p l e . |
A body is thrown upwards;
h
is its height over a ground,
t
is the time, passed
from a throwing moment.
h is a single-valued function of t , but t is a two-valued function of h , because the body is on the same height twice: the first time at an assent, the second time at a fall. The formula |
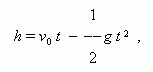
binding variables h and t ( initial velocity v 0 and an acceleration of a gravity g are constants here ), shows that we have only one value of h at the given t , and two values of t at the given h ( they are determined by solving the quadratic equation ).