Representation of function by formula and table
Many of functions can be represented ( exactly or approximately ) by simple formulas. For example, the dependence between an area
S
of a circle and its radius
r
is given by the formula
S
=
r
2
; the previous example shows the dependence between a height
h
of a thrown body and a flying time
t
. But this formula is in fact an approximate one,
because it does not consider neither a resistance of air nor a weakening of Earth gravity by a height. It is very often impossible to
represent a functional dependence by a formula, or this formula is an uncomfortable for calculations. In these cases a function is
represented by a table or a graph.
E x a m p l e . The functional dependence between a pressure
p
and a temperature of water
boiling
T
cannot be presented by the one formula, so it is
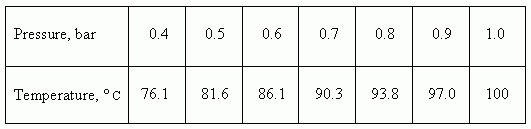
It is obvious, that any table cannot contain all values of argument, but an available for practice table must contain so many values, that they are enough to work or to receive additional values by interpolating the existing ones.