Composite function


Consider the function:

y = sin 2 ( 2 x ) .

Actually, this record means the following chain of functional transformations:

u = 2 x --> v = sin u --> y = v 2 ,

that can be written by symbols of functional dependences in a general view as:

u = f 1 ( x ) --> v = f 2 ( u ) --> y = f 3 ( v ) ,

or more shortly:

y = f { v [ u ( x ) ] }.

We have here not the one rule of correspondence to transform x into y , but  three consecutive rules (functions), using which we receive y from x . In this case we say that y is a composite function of x .

E x a m p l e .  The following functions are composite ones:

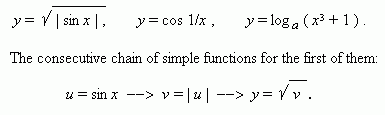
Write, please, the two rest functions like this.

Back