Inscribed and circumscribed polygons. Regular polygons

Inscribed polygon in a circle is a polygon, vertices of which are placed on a circumference ( Fig.54 ) . Polygon circumscribed around a circle is a polygon, sides of which are tangents to the circumference ( Fig.55 ) .

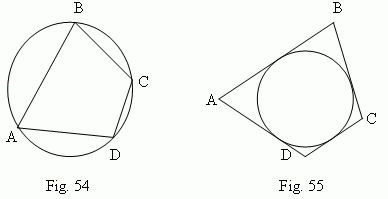
Correspondingly, a circumference, going through vertices of a polygon ( Fig.54 ), is called a circumcircle around a polygon ; a circumference, for which sides of a polygon are tangents ( Fig.55 ), is called an incircle into a polygon. For an arbitrary polygon it is impossible to inscribe a circle in it and to circumscribe a circle around it. For a triangle it is always possible . A radius  r  of an incircle is expressed by sides a, b, c of a triangle as:

A radius  R  of a circumcircle is expressed by the formula:

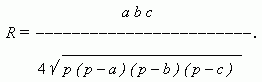
It is possible to inscribe a circle in a quadrangle , if sums of its opposite sides are the same. In case of parallelograms it is valid only for a rhombus (a square). A center of an inscribed circle is placed in a point of intersection of diagonals. It is possible to circumscribe a circle around a quadrangle , if a sum of its opposite angles is equal to 180 deg. In case of parallelograms it is valid only for a  rectangular (a square). A center of a circumscribed circle is placed in a point of intersection of diagonals. It is possible to circumscribe a circle around a trapezoid, only if  it is an isosceles one.

Regular polygon is a polygon with equal sides and angles

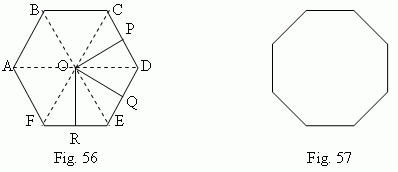
On Fig.56 a regular hexagon is shown, on Fig.57 – a regular octagon. A regular quadrangle is a square; a regular triangle is an equilateral triangle. Each angle of a regular polygon is equal to 180 ( n – 2 ) / n deg, where n is a number of angles. There is a point O ( Fig. 56 ) inside of a regular polygon, equally removed from all its vertices ( OA = OB = OC = … = OF ), which is called a center of a regular polygon. The center is also equally removed from all the sides of a regular polygon ( OP = OQ = OR = … ). The segments OP, OQ, OR, … are called apothems ; the segments OA, OB, OC, … – radii of a regular polygon. It is possible to inscribe a circle in a regular polygon and to circumscribe a circle around it. The centers of inscribed and circumscribed circles coincide with a center of a regular polygon. A radius of a circumscribed circle is a radius of a regular polygon, a radius of a inscribed circle is its apothem. The following formulas are relations between sides and radii of regular polygon:

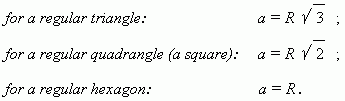
For the most of regular polygons it is impossible to express the relation between their sides and radii by an algebraic formula.

E x a m p l e . Is it possible to cut out a square with a side 30 cm from a circle with a diameter
40 cm ?

S o l u t i o n . The biggest square, included in a circle, is an inscribed square. According
to the above mentioned formula its side is equal:

Hence, it is impossible to cut out a square with a side 30 cm from a circle with
a diameter 40 cm.