Cone

Conic surface is a surface, formed by a motion of a straight line ( AB, Fig.85 ), which goes constantly through an immovable point ( S ), and intersects with the given line  MN, which is called a directrix . Straight lines, corresponding to different positions of the straight line AB at its motion  ( A’B’,  A”B” etc. ), are called generatrices of a conic surface. The point S is a vertex of a conic surface. A conic surface has two parts: one is drawn by the ray SA, another – by its continuation SB. Often it is implied, that a conic surface is one of its parts.

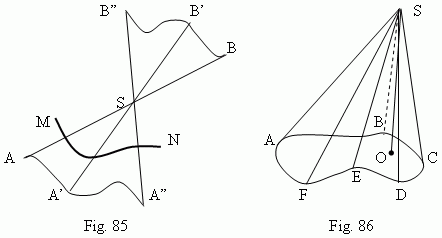
Cone is a body, limited by one of parts of a conic surface  ( with a closed directrix ) and a plane, intersecting it (ABCDEF, Fig.86 ) and which doesn’t go through a vertex  S. A part of this plane, placed inside of the conic surface, is called a base of cone. The perpendicular  SO, drawn from a vertex S to a base, is called a height of cone. A pyramid is a particular shape of a cone ( why ? ). A cone is circular , if its base is a circle. The straight line SO, joining a cone vertex with a center of a base, is called an axis of a cone. If a height of circular cone coincides with its axis, then this cone is called a round cone.

Conic sections. The sections of circular cone, parallel to its base, are circles. The section, crossing only one part of a circular cone and not parallel to single its generatrix, is an ellipse ( Fig.87 ). The section, crossing only one part of a circular cone and parallel to one of its generatrices, is a parabola ( Fig.88 ). In a general case the section, crossing both parts of a circular cone , is a hyperbola , consisting of two branches ( Fig.89 ) . Particularly, if this section is going through the cone axis , then we receive a pair of intersecting straight lines .

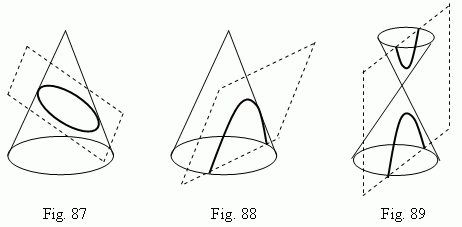
Conic sections are of a great interest both in a theoretical and in a practical relation. So, we use them in a technique ( gears, parabolic searchlights and antennae). Planets and some comets move along elliptic orbits; some comets move along parabolic and hyperbolic orbits.