Tangent plane of a ball, a cylinder and a cone

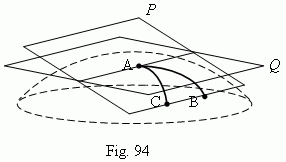
Consider three points A, B, C on a some curved surface ( Fig. 94 ) and draw through them the crossing plane P . Two points B and C we’ll move to point A  along the two different directions. Then, the plane P will approach the some position Q independently on a place, where points B and C have been taken, and a path of their moving to point  A. The plane Q is called a tangent plane in point A. It is  possible, that there is not a tangent plane in some point of a surface. For example, a conic surface has no a tangent plane in a vertex of a cone.

The plane P, which is a tangent plane of a spherical surface ( Fig.95 ), is perpendicular to radius OA, drawn to the tangency point A; a tangent plane of a spherical surface has only one common point with the surface – a tangency point.

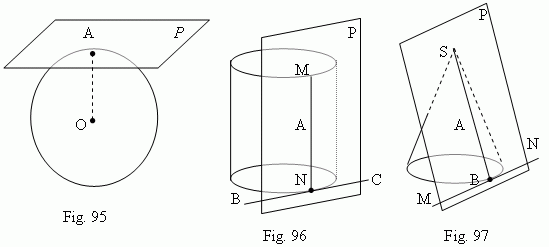
The plane P, which is a tangent plane to a surface of a round cylinder in the point  A ( Fig.96 ), goes through the generatrix  MN, containing the point A, and a tangent line BC of a base circle, containing the point N. A plane, tangent to a surface of a round cylinder is removed from all points of its axis by a distance, equal to radius of a cylinder base. The plane P, which is a tangent plane to a surface of a round cone in the point A, which doesn’t coincide with the vertex S ( Fig.97 ), goes through the generatrix  SB, containing the point A, and a tangent line MN of a base circle, containing the point B. A cylinder is called an inscribed into a prism , if lateral faces of the prism are planes, tangent to the cylinder, and planes of their bases are the same. A cylinder is called a circumscribed around a prism , if lateral edges of the prism are generatrices of a lateral surface of a cylinder, and planes of their bases are the same.

A cone is called an inscribed into a pyramid , if lateral faces of the pyramid are planes, tangent to the cone, and planes of their bases are the same. A cone is called a circumscribed about a pyramid , if lateral edges of the pyramid are generatrices of a lateral surface of a cone, and planes of their bases are the same.