Symmetry. Symmetry of plane figures

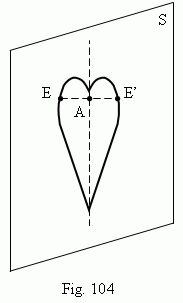
Mirror symmetry. A geometric figure is called a symmetrical relatively a plane S ( Fig.104 ), if for each point E of this figure a point E’of the same figure can be found, so that a segment  EE’ is perpendicular to a plane S and is divided by this  plane into two ( EA = AE’ ). A plane S is called a symmetry plane . Symmetrical figures, subjects and bodies are nor equal one to another in a narrow meaning ( for instance, a left glove is not suitable for a right hand and vice versa ). They  are called mirror equal .

Central symmetry. A geometric figure (or a body) is called a symmetrical relatively a center C ( Fig.105 ), if for each point  A of this figure the point E of the same figure can be found, so that a segment AE goes through the center C and is divided in this point into two (AC = CE). A point C is called a symmetry center .

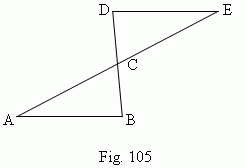
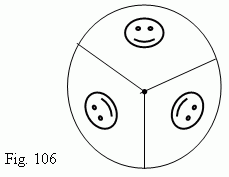
Rotation symmetry. A body (a figure) has a rotation symmetry ( Fig.106 ), if  at turning by an angle 360 °/ n ( here n – integer ) around some straight line AB ( symmetry axis ) it coincides completely with its initial position. At n = 2 we have an axial symmetry. Triangles  ( Fig.105 ) have also an axial symmetry.

Examples of above mentioned kinds of symmetry. A sphere  ( ball ) has a central, a mirror and a rotation symmetry. A symmetry center is a center of a ball; a symmetry plane is a plane of any large circle; a symmetry axis is a diameter of a ball. A round cone has an axial symmetry; a symmetry axis is an axis of a cone. A right prism has a mirror symmetry. A symmetry plane is parallel to its bases and placed by equal distance between them.

Symmetry of plane figures. Mirror-axial symmetry. If the plane figure ABCDE  ( Fig.107 ) is symmetrical relatively a plane S ( that is possible only if the figure plane is perpendicular to the plane S ), then the straight line KL, along which these planes are intersected, is a symmetry axis of the 2-nd order of the figure ABCDE. In this case the figure ABCDE is called a mirror symmetrical one.

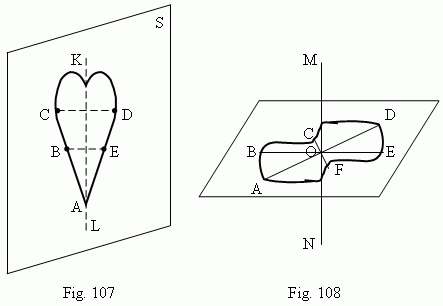
Central symmetry. If the plane figure ( ABCDEF,  Fig.108 ) has a symmetry axis of the 2-nd order, perpendicular to the figure plane (a straight line MN,  Fig.108 ), then a point O, in which MN and the figure plane ABCDEF intersect, is a symmetry center .

Examples of symmetry of plane figures.
A parallelogram has only a central symmetry. Its symmetry center is a point of ntersection of diagonals. An isosceles trapezoid has only an axis symmetry. Its symmetry axis is a perpendicular, drawn through middles of its bases. A rhombus has both a central and an axial symmetry. Its symmetry axis is any of its diagonals; a symmetry center is a point of their intersection. A circle has … What can you say about a circle’s kinds of symmetry ?