Angles
Right (direct), acute and obtuse angle. Mutually
perpendicular straight lines. Signs of angles.
Supplementary (adjacent) angles. Vertically
opposite (vertical) angles. Bisector of an angle.
Angle
is a geometric figure ( Fig.1 ), formed by two rays OA and OB (
sides of an angle
), going out of the same point O (a
vertex of an angle
).
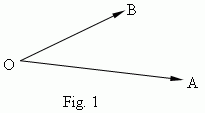
An angle is signed by the symbol
and three letters, marking ends of rays and a vertex of an angle:
AOB (moreover, a vertex letter is placed in the middle). A
measure of an angle
is a value of a turn around a vertex O, that transfers a ray OA to the position OB. Two units of angles measures are widely used: a
radian
and a
degree
. About a radian measure see
below in the point "A length of arc"
and also
in the section "Trigonometry"
.
A
degree measure.
Here a unit of measurement is a
degree
( its designation is ° or
deg
)
–
a turn of a ray by the 1/360 part of the one complete revolution. So, the complete revolution of a ray is equal to 360 deg. One degree is divided by 60
minutes
( a designation is ‘ or
min
); one minute – correspondingly by 60
seconds
( a designation is “ or
sec
).An angle of 90 deg ( Fig.2 ) is called a
right
or
direct
angle; an angle lesser than 90 deg ( Fig.3 ), is called an
acute
angle; an angle greater than 90 deg ( Fig.4 ), is called an
obtuse
angle.
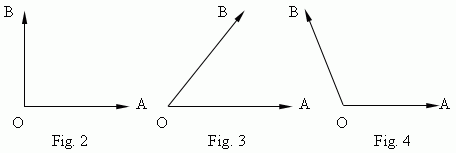
Straight lines, forming a right angle, are called
mutually perpendicular
lines. If the straight lines AB and MK are perpendicular, this is signed as: AB
MK.
Signs of angles.
An angle is considered as
positive
, if a rotation is executed
opposite a clockwise
, and
negative
– otherwise. For example, if the ray OA displaces to the ray OB as shown on Fig.2, then
AOB = + 90 deg; but on Fig.5
AOB = – 90 deg.
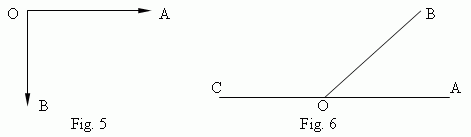
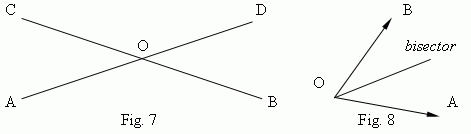
Supplementary (adjacent) angles ( Fig.6 ) – angles AOB and COB, having the common vertex O and the common side OB;
other two sides OA and OC form a continuation one to another. So, a sum of supplementary (adjacent) angles is equal to 180 deg.Vertically opposite (vertical) angles ( Fig.7) – such two angles with a common vertex, that sides of one angle are continuations of the other:
AOB and
COD ( and also
AOC and
DOB ) are vertical angles.
A
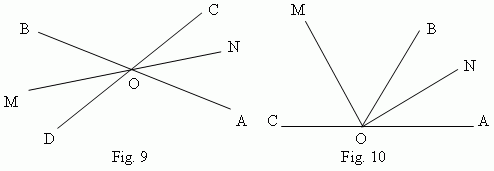
bisector
of an angle is a ray, dividing the angle in two ( Fig.8 ). Bisectors of vertical angles (OM and ON, Fig.9) are continuations one of the other. Bisectors of supplementary angles (OM and ON, Fig.10) are mutually perpendicular lines.
The property of an angle bisector: any point of an angle bisector is placed by the same distance from the angle sides .