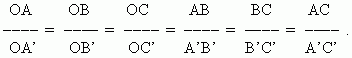Parallel straight lines
Angles with correspondingly parallel sides. Corresponding angles.
Alternate interior and exterior angles. One-sided interior and
exterior angles. Angles with correspondingly perpendicular sides.
Proportional segments. Thales' theorem.
Two straight lines AB and CD ( Fig.11 ) are called parallel straight lines , if they lie in the same plane and don’t intersect however long they may be continued. The designation: AB || CD. All points of one line are equidistant from another line. All straight lines, parallel to one straight line are parallel between themselves. It’s adopted that an angle between parallel straight lines is equal to zero. An angle between two parallel rays is equal to zero, if their directions are the same, and 180 deg, if the directions are opposite. All perpendiculars (AB, CD, EF, Fig.12) to the one straight line KM are parallel between themselves. Inversely, the straight line KM, which is perpendicular to one of parallel straight lines, is perpendicular to all others. A length of perpendicular segment, concluded between two parallel straight lines, is a distance between them.
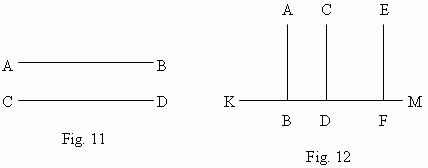
At intersecting two parallel straight lines by the third line, eight angles are formed ( Fig.13 ), which are called two-by-two:
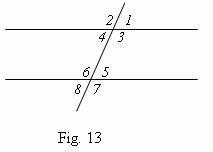
1)
corresponding angles
(
1
and
5; 2
and
6; 3
and
7; 4
and
8
); these angles
are equal two-by-two: (
1 =
5;
2
=
6;
3
=
7;
4
=
8
);
2)
alternate interior angles
(
4
and
5; 3
and
6
); they are equal two-by-two;
3)
alternate exterior angles
(
1
and
8; 2
and
7
); they are equal two-by-two;
4)
one-sided interior angles
(
3
and
5; 4
and
6
); a sum of them two-by-two
is equal to180 deg (
3
+
5 =
180 deg;
4
+
6
= 180 deg);
5)
one-sided exterior angles
(
1
and
7; 2
and
8
); a sum of them two-by-two
is equal to180 deg (
1
+
7
= 180 deg;
2
+
8
= 180 deg).
Angles with
correspondingly parallel sides
either are equal one to another, ( if both of them are acute or both are obtuse,
1 =
2
, Fig.14 ), or sum of them is 180 deg (
3
+
4 =
180 deg, Fig.15 ).
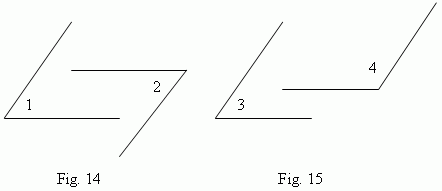
Angles with correspondingly perpendicular sides are also either equal one to another ( if both of them are acute or both are obtuse ), or sum of them is 180 deg.
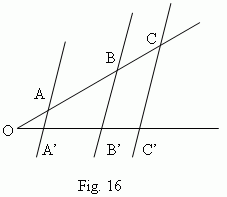
Thales' theorem. At intersecting sides of an angle by parallel lines (
Fig.16 ), the angle sides are divided into the proportional segments:
