Parallelogram and trapezoid

Parallelogram ( ABCD,  Fig.32 ) is a quadrangle, opposite sides of which are two-by-two parallel.

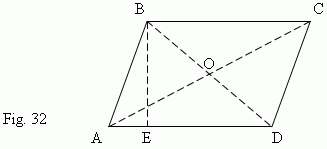
Any two opposite sides of a parallelogram are called bases , a distance between them is called a height ( BE,  Fig.32 ).

Properties of a parallelogram.

1. Opposite sides of a parallelogram are equal ( AB = CD, AD = BC ).

2. Opposite angles of a parallelogram are equal ( A = C, B = D ).

3. Diagonals of a parallelogram are divided in their intersection point into two
( AO = OC, BO = OD ).

4. A sum of squares of diagonals is equal to a sum of squares of four sides :
AC ² + BD ² = AB ² + BC ² + CD ² + AD ² .

Signs of a parallelogram.

A quadrangle is a parallelogram, if one of the following conditions takes place:

1. Opposite sides are equal two-by-two ( AB = CD, AD = BC ).

2. Opposite angles are equal two-by-two ( A = C, B = D ).

3. Two opposite sides are equal and parallel ( AB = CD, AB || CD ).

4. Diagonals are divided in their intersection point into two ( AO = OC, BO = OD ).

Rectangle.

If one of angles of parallelogram is right, then all angles are right (why ?). This parallelogram is called a rectangle ( Fig.33 ).

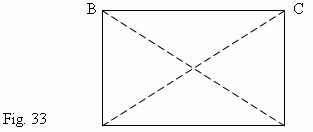
Main properties of a rectangle.

Sides of rectangle are its heights simultaneously.

Diagonals of a rectangle are equal: AC = BD.

A square of a diagonal length is equal to a sum of squares of its sides’ lengths ( see above Pythagorean theorem ):

Rhombus. If all sides of parallelogram are equal, then this parallelogram is called a rhombus ( Fig.34 ) .

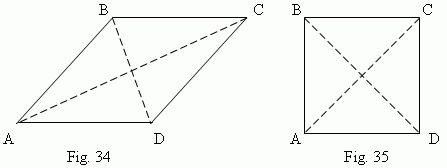
Diagonals of a rhombus are mutually perpendicular ( AC BD ) and divide its angles into two ( DCA = BCA, ABD = CBD etc. ).

Square is a parallelogram with right angles and equal sides ( Fig.35 ). A square is a particular case of a rectangle and a rhombus simultaneously; so, it has all their above mentioned properties.

Trapezoid is a quadrangle, two opposite sides of which are parallel  (Fig.36).

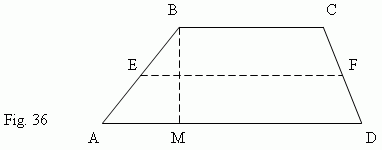
Here AD || BC.  Parallel sides are called bases of a trapezoid, the two others ( AB and CD ) – lateral sides. A distance between bases (BM) is a height. The segment EF, joining midpoints E and F of the lateral sides, is called a midline of a trapezoid.
A midline of a trapezoid is equal to a half-sum of bases:

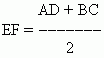
and parallel to them: EF || AD and EF || BC.
A trapezoid with equal lateral sides ( AB = CD ) is called an isosceles trapezoid. In an isosceles trapezoid angles by each base, are equal ( A = D, B = C ). A parallelogram can be considered as a particular case of trapezoid.

Midline of a triangle is a segment, joining midpoints of lateral sides of a triangle. A midline of a triangle is equal to half of  its base and parallel to it. This property follows from the previous part, as triangle can be considered as a limit case (“degeneration”) of a trapezoid, when one of its bases transforms to a point.