Similarity of plane figures. Similarity criteria of triangles
Similarity of polygons. Similarity of triangles.
Similarity of right-angled triangles.
Similarity of plane figures.
If to change ( to increase or to decrease ) all sizes of a plane figure in the same ratio (
ratio of similarity
), then an old and a new figures are called
similar
ones. For example, a picture and its photograph are similar figures.
In two similar figures any corresponding angles are equal, that is, if points A, B, C, D of one figure correspond to points
a, b, c, d
of another figure, then
ABC =
abc
,
BCD =
bcd
and so on.
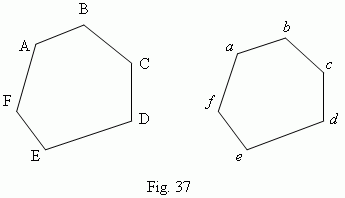
Two polygons
( ABCDEF and
abcdef
, Fig.37 )
are similar, if their angles are equal:
A =
a ,
B =
b , …,
F =
f , and sides are proportional:
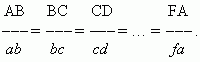
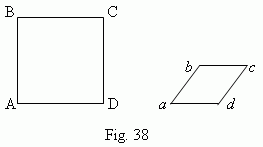
Only proportionality of sides is not enough for similarity of polygons. For example, the square ABCD and the rhombus abcd ( Fig.38 ) have proportional sides: each side of the square is twice more than of the rhombus, but the diagonals have not changed proportionally.
But, for similarity of triangles proportionality of its sides is enough.
Similarity criteria of triangles. Two triangles are similar, if:
| 1) |
all their corresponding angles are equal;
|
| 2) |
all their sides are proportional;
|
| 3) | two sides of one triangle are proportional to two sides of another and the angles concluded between these sides are equal. |
Two right-angled triangles are similar, if
| 1) |
their legs are proportional;
|
| 2) |
a leg and a hypotenuse of one triangle are proportional to a leg and a hypotenuse
of another;
|
| 3) | two angles of one triangle are equal to two angles of another. |
Areas of similar figures are proportional to squares of their resembling lines ( for instance, sides ). So, areas of circles are proportional to ratio of squares of diameters ( or radii ).
| E x a m p l e . |
A round metallic disc by diameter 20 cm weighs 6.4 kg. What is the weight of a round metallic disc by diameter 10 cm ?
|
| S o l u t i o n . |
Because the material and the thick of a new disc are the same, the weights of
the discs are proportional to their areas, and a ratio of an area of the small disc
to an area of the big disc is equal to:
Hence, the weight of the small disc is 6.4 · 0.25 = 1.6 kg. |