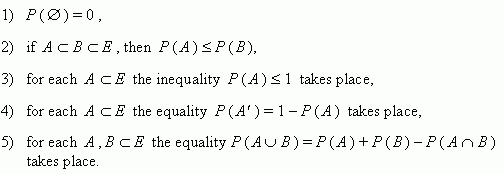Definition and basic properties of probability
Axiomatic and classical definitions of probability.
Probability of event. Basic properties of probability.
The axiomatic definition of
probability.
Let a
space of elementary events
E
be
given
and such single number
Ð
(
À
)
corresponds to each event
À
![]() Å
, that:
Å
, that:
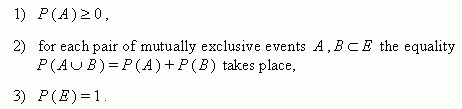
Then we say, that the probability is defined on events of E , and the number Ð ( À ) is called the probability of an event A .
The classical definition of probability . Let a space of elementary events E be given and this space consists of N equally likely elementary events, among which there are n events, favorable for an event A . Then the number
Ð ( À ) = n / N
is called the probability of an event A .
Basic properties of probability . Let a space of elementary events E be given and probabilities P are defined on events of E . Then: