Random variables
Random variable. Discrete and continuous random variables.
Independent random variables. Density function.
Distribution function. General properties of distribution function.
A variable is called random , if it can receive real values with definite probabilities as a result of experiment. The random variable X is called discrete , if such non-negative function exists
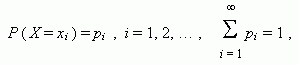
which determines the correspondence between a value õ i of the variable Õ and the probability ð i , that X receives this value.
Discrete random variables X and Y are called independent random variables , if the events Õ = õ i and Y = y j are independent for arbitrary i and j .
The random variable X is called a continuous random variable , if for any numbers a < b such non-negative function f ( x ) exists, that
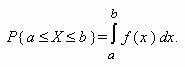
The function f ( x ) is called a density function of continuous random variable . The probability of the fact that a random variable X receives a value less than x , is called a distribution function of random variable X and marked as F ( x ) :
F
(
x
) =
Ð
(
X
![]() x
) .
x
) .
General properties of distribution function:
