Operations with sets
Designation of sets and their elements. Equality of sets.
Subset ( inclusion ). Sum ( union ) of sets.
Product ( intersection ) of sets. Difference ( complement ) of sets.
Symmetric difference of sets. Properties of operations with sets.
Sets are designated by capital
letters, and their elements – by small letters. The
record
a
R
means, that an element
à
belongs to a set
R
,
i.e.
à
is an element of the set
R
. Otherwise, if
à
doesn't belong to the set
R
, we write
a
R
.
Two sets À and B are called equal ( À =  ), if they consist of the same elements, i.e. each element of the set A is an element of the set B and vice versa, each element of the set  is an element of the set A .
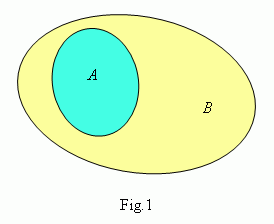
We
say,
that a set
À
is
included in a set
Â
(
Fig.1
)
or the
set
A
is
a
subset
of the set
B
(
in this case we write
À
Â
),
if each element of the set
A
is an element of the set
B
. This dependence between sets is
called an
inclusion
. The inclusions
À
and
À
À
take place for each set
A
.
A
sum (
union
)
of sets
À
and
Â
(
it's
written
as
À
Â
)
is
a
set
of elements,
each
of them
belongs
either
to
A
,
or
to
B
. So,
å
À
Â
,
if and only if
either
å
À
,
or
å
Â
.
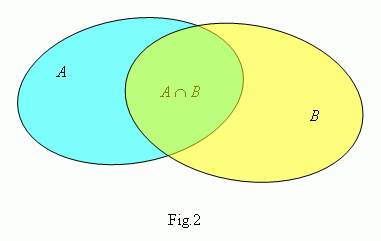
A product (
intersection
) of sets
À
and
Â
(
it's written as
À
Â
, Fig.2 ) is a set of
elements, each of them belongs both to
À
and to
Â
. So,
å
À
Â
,
if and only if
å
À
and
å
Â
.
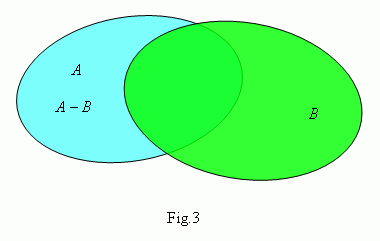
A difference of sets À and  ( it's written as À –  , Fig.3 ) is a set of elements, which belong to the set A , but don't belong to the set  . This set is called also a complement of the set B relatively the set A .
A symmetric difference of sets A and B ( it's written as À \ Â ), is called a set:
À
\
Â
= (
A
–
B
)
(
Â
–
A
) .
Properties of operations with sets:
E x a m p l e s. 1. A set of children is a subset of the whole population.
2. An intersection of the set of integers and the set of positive
numbers is the set of natural numbers.
3. A union of the set of rational numbers and the set of irrational
numbers is the set of real numbers.
4. Zero is a complement of the set of natural numbers relatively
the set of non-negative integers.