Solving of oblique triangles
| Case 1. |
Three sides
a, b, c
are given. Find angles
A, B, C.
By the law of cosines we find one of the angles:
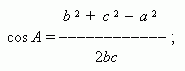
the second angle we find by the law of sines: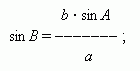 
the third angle is found by the formula: C = 180° – ( A + B ). |
| E x a m p l e . |
Three sides of a triangle are given:
a
= 2,
b
= 3,
c
= 4. Find angles of this triangle.
|
| S o l u t i o n . |
|
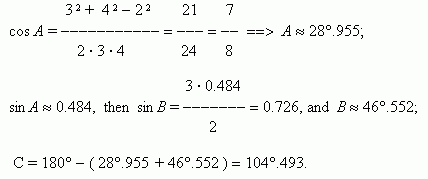
| Case 2. |
Given: two sides
a
and
b
and angle
C
between them. Find a side
c
and
angles
A
and
B
. By the law of cosines we find a side
c
:
and then by the law of sines – an angle A :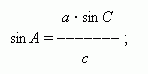 
here it is necessary to emphasize that A is an acute angle, if b / a > cos C , and an obtuse angle, if b / a < cos C . The third angle B = 180° – ( A + C ). |
| Case 3. | Any two angles and a side are given. Find the third angle and two other sides. It is obvious, that the third angle is calculated by the formula: A+ B+ C = 180°, and then using the law of sines we find two other sides. |
| Case 4. |
Given two sides
a
and
b
and angle
B
, opposite one of them. Find a side
c
and
angles
A
and
C
. At first by the law of sines we find an angle
A
:
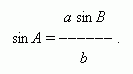
The following cases are possible here: 1) a > b ; a · sin B > b – there is no solution here; 2) a > b ; a · sin B = b – there is one solution here, A is a right angle; 3) a > b ; a · sin B < b < a – there are two solutions here: A may be taken either an acute or an obtuse angle; 4) a 
b
– there is one solution here,
A
– an acute angle.
After determining an angle
A
, we find the third angle:
C = 180° – ( A+ B ). Ii is obvious that if A can have two values, then also C can have two values. Now the third side can be determined by the law of sines: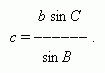 
If we found two values for C , then also a side c has two values, hence, two different triangles satisfy the given conditions. |
| E x a m p l e . |
Given:
a
= 5,
b
= 3,
B
= 30°. Find a side
c
and angles
A
and
C
.
|
| S o l u t i o n . |
We have here:
a > b
and
a
sin
B < b .
( Check it please ! ).
Hence, according to the case 3 two solutions are possible here: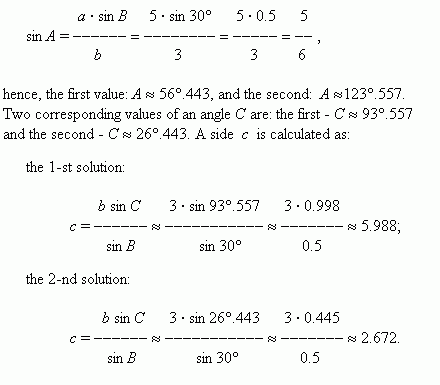 
|