Inverse trigonometric functions
Principal values of inverse trigonometric functions.
The relation
x
= sin
y
permits to find both
x
by the given
y
, and also
y
by the given
x
( at |
x
|
1 ). So, it is possible to consider not only a sine as a function
of an angle, but an angle as a function of a sine. The last fact can be written as:
y
= arcsin
x
( “arcsin” is read as “arcsine” ). For instance, instead
of 1/2 = sin 30° it is possible to write: 30° = arcsin 1/2. At the second record form an angle is usually represented in a radian measure:
/ 6 = arcsin 1/2.
Definitions.
arcsin
x
is an angle, a sine of which is equal to
x
.
Analogously the functions
arccos
x
,
arctan
x
,
arccot
x
,
arcsec
x
,
arccosec
x
are defined.
These functions are inverse to the functions sin
x
, cos
x
, tan
x
, cot
x
, sec
x
,
cosec
x
, therefore they are called
inverse trigonometric functions.
All inverse trigonometric functions are
multiple-valued functions
, that
is to say for one value of argument an innumerable set of a function values is in accordance. So, for example, angles 30°,
150°, 390°, 510°, 750° have the same sine. A
principal value
of arcsin
x
is that its value, which is contained between
–
/ 2 and +
/ 2
( –90° and +90° ),
including the bounds
:
/ 2
arcsin
x
+
/ 2 .
A
principal value
of arccos
x
is that its value, which is contained between 0 and
( 0° and +180° ),
including the bounds
:
arccos
x
.
A
principal value
of arctan
x
is that its value, which is contained between –
/
2 and +
/ 2 (
–90° and +90° )
without the bounds
:
/ 2 < arctan
x
< +
/ 2 .
A
principal value
of arccot
x
is that its value, which is contained between 0 and
( 0° and +180° )
without the bounds
:
.
If to sign any of values of inverse trigonometric functions as Arcsin x , Arccos x , Arctan x , Arccot x and to save the designations: arcsin x , arcos x , arctan x , arccot x for their principal values, then there are the following relations between them:
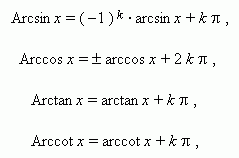
where k – any integer. At k = 0 we have principal values.