Trigonometric equations. Main methods for solving

Trigonometric equations. Simplest trigonometric equations.
Methods of solving:  algebraic method,  factoring, reducing
to a homogeneous equation, transition to a half-angle,
introducing an auxiliary angle, transforming a product to
a sum, universal substitution.

Trigonometric equations. An equation, containing an unknown under the trigonometric function sign is called trigonometric .

Simplest trigonometric equations.







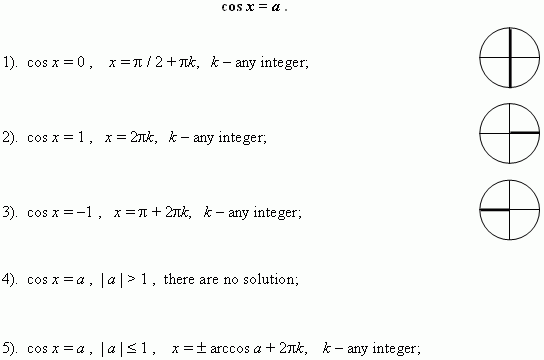
Methods for solving trigonometric equations. Solving of a trigonometric equation consists of the two stages: transforming of a equation to receive its simplest shape ( see above ) and solving of the received simplest trigonometric equation. There are seven main methods of solution of trigonometric equations.

1. Algebraic method. This method is well known for us from algebra ( exchange and
substitution method ).

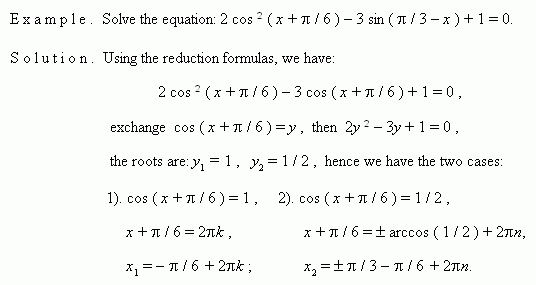
2. Factoring. Consider this method by examples.

E x a m p l e  1.  Solve the equation:  sin x + cos x = 1 .

S o l u t i o n .    Transfer all terms to the left:

sin x + cos x – 1 = 0 ,

transform and factor the left-hand side expression:

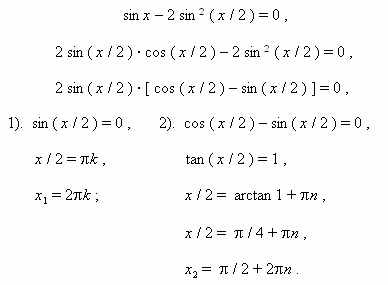
E x a m p l e  2.  Solve the equation:  cos ² x + sin x · cos x = 1.

S o l u t i o n .     cos ² x + sin x · cos x – sin ² x – cos ² x = 0 ,

sin x · cos x – sin ² x = 0 ,

sin x · ( cos x – sin x ) = 0 ,

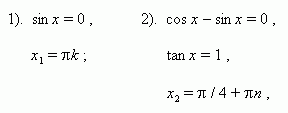
E x a m p l e  3.  Solve the equation:  cos 2 x – cos 8 x + cos 6 x = 1.

S o l u t i o n .     cos 2 x + cos 6 x = 1 + cos 8 x ,

2 cos 4 x cos 2 x = 2 cos ² 4 x ,

cos 4 x · ( cos 2 x –  cos 4 x ) = 0 ,

cos 4 x · 2 sin 3 x · sin x = 0 ,

1).  cos 4 x = 0 ,               2).  sin 3 x = 0 ,          3). sin x = 0 ,

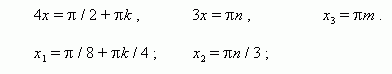
3. Reducing to a homogeneous equation. An equation is called a homogeneous equation in sin and cos , if and only if all its terms are of the same degree in sin and cos of the same angle.
To solve the homogeneous equation it is necessary:
a )  to transfer all terms to the left-hand side;
b )  to take all common factors out of brackets;
c )  to equate all factors and brackets to zero;
d )  the brackets equated to zero give the homogeneous equation of the smaller
degree, which should be divided by cos ( or sin ) of the higher power;
e )  to solve the received algebraic equation in tan .

E x a m p l e .  Solve the equation: 3 sin ² x + 4 sin x · cos x + 5 cos ² x = 2.

S o l u t i o n .  3 sin ² x + 4 sin x · cos x + 5 cos ² x = 2sin ² x + 2cos ² x ,

sin ² x + 4 sin x · cos x + 3 cos ² x = 0 ,

tan ² x + 4 tan x + 3 = 0 ,  hence y ² + 4 y +3 = 0 ,

the roots of this equation are: y 1 = –1 , y 2 = –3 ,  from here

1)   tan x = –1, 2)   tan x = –3,