Trigonometric functions of an acute angle

Trigonometric functions of an acute angle are ratios of different pairs of sides of a right-angled triangle ( Fig.2 ).

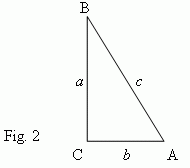
1) Sine: sin A = a / c ( a ratio of an opposite leg o a hypotenuse ) .

2) Cosine: cos A = b / c ( a ratio of an adjacent leg to a hypotenuse ) .

3) Tangent: tan A = a / b ( a ratio of an opposite leg to an adjacent leg ) .

4) Cotangent: cot A = b / a ( a ratio of an adjacent leg to an opposite leg ) .

5) Secant: sec A = c / b ( a ratio of a hypotenuse to an adjacent leg ) .

6) Cosecant: cosec A = c / a ( a ratio of a hypotenuse to an opposite leg ) .

There are analogous formulas for another acute angle B ( Write them, please ! ).

E x a m p l e .  A right-angled triangle ABC  ( Fig.2 ) has the following legs:
a = 4, b = 3. Find sine, cosine and tangent of angle A.

S o l u t i o n .  At first we find a hypotenuse, using Pythagorean theorem:

c ² = a ² + b ² ,

According to the above mentioned formulas we have:
sin A = a / c = 4 / 5;  cos A = b / c = 3 / 5;  tan A = a / b = 4 / 3.

For some angles it is possible to write exact values of their trigonometric functions. The most important cases are presented in the table:

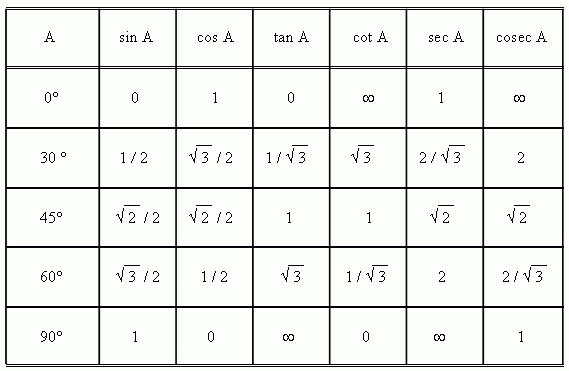
Although angles 0° and 90° cannot be acute in a right-angled triangle, but at enlargement of notion of trigonometric functions ( see below), also these angles are considered. A symbol in the table means that absolute value of the function increases unboundedly, if the angle approaches the shown value.