Trigonometric functions of any angle

To build all trigonometry, laws of which would be valid for any angles ( not only for acute angles, but also for obtuse, positive and negative angles), it is necessary to consider so called a unit circle , that is a circle with a radius, equal to 1 ( Fig.3 ).

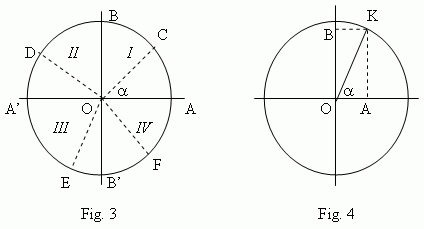
Let draw two diameters: a horizontal AA’ and a vertical BB’. We count angles off a point A (starting point). Negative angles are counted in a clockwise, positive in an opposite direction. A movable radius OC forms angle with an immovable radius OA. It can be placed in the 1-st quarter ( COA ), in the 2-nd quarter ( DOA ), in the 3-rd quarter ( EOA ) or in the 4-th quarter ( FOA ). Considering OA  and  OB  as positive directions and  OA’  and  OB’ as negative ones, we determine trigonometric functions of angles as follows.

A sine line of an angle ( Fig.4 ) is a vertical diameter of a unit circle, a cosine line of an angle - a horizontal diameter of a unit circle. A sine of an angle ( Fig.4 ) is the segment OB of a sine line, that is a projection of a movable radius OK to a sine line; a cosine of an angle - the segment OA of a cosine line, that is a projection of a movable radius OK to a cosine line.

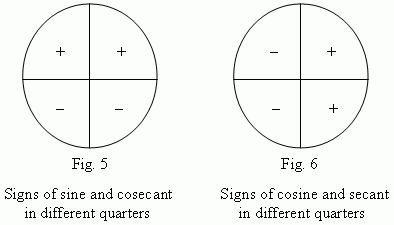
Signs of sine and cosine in different quarters of a unit circle are shown on Fig.5 and Fig.6.

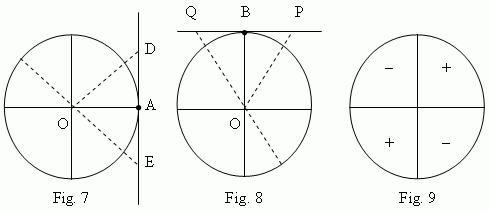
A tangent line ( Fig.7 ) is a tangent, drawn to a unit circle through the point A of a horizontal diameter.
A cotangent line ( Fig.8 ) is a tangent, drawn to a unit circle through the point B of a vertical diameter.
A tangent is a segment of a tangent line between the tangency point A and an intersection point ( D, E, etc., Fig.7 ) of a tangent line and a radius line.
A cotangent is a segment of a cotangent line between the tangency point B and an intersection point ( P, Q, etc., Fig.8 ) of a cotangent line and a radius line.

Signs of tangent and cotangent in different quarters of a unit circle see on Fig.9.

Secant and cosecant are determined as reciprocal values of cosine and sine correspondingly.