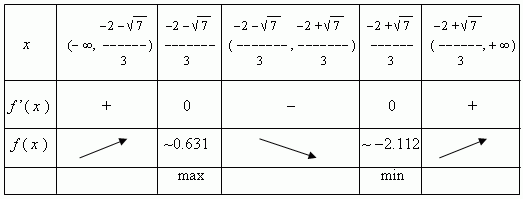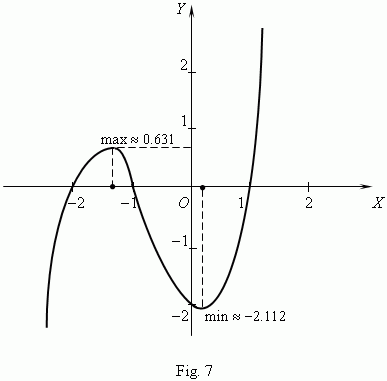Application of derivative in investigation of functions
conditions of functions monotony. Darboux's theorem.
Intervals of function monotony. Critical points.
Extreme ( minimum, maximum ). Points of extreme.
Necessary condition of extreme. Sufficient conditions
of extreme. Plan of function investigation.
Relation between continuity and differentiability of function.
If a function
is differentiable at some point, then it is a continuous function at this point. Contrary is invalid: a continuous function can have no derivative.
C o n s e q u e n c e .
If a function is discontinuous at some point,
then it has
no derivative in this point.
| E x a m p l e . |
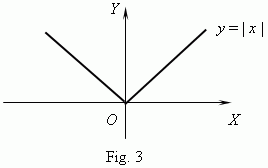
The function
y
= |
x
| ( Fig.3 ) is continuous everywhere, but it has no derivative at
x
= 0 ,
because a tangent of the graph at this point does not exist. ( think, please, why ? ) |
Sufficient conditions of functions monotony.
If f
’(
x
)
> 0 at every point of an interval
(
a, b
)
, then a function f
(
x
)
increases within this interval.
If f
’(
x
)
< 0 at every point of an interval
(
a, b
)
, then a function f
(
x
)
decreases within this interval.
Darboux’s theorem. Points, at which a derivative of a function is equal to 0 or doesn’t exist, divide a function domain for such intervals that within each of them a derivative saves a constant sign.
Using these signs it is possible to find intervals of monotony of functions, what is very important in investigations of functions.

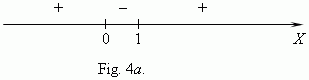
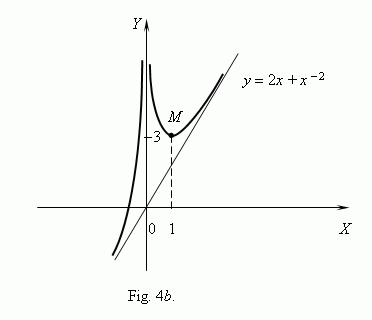
Hence, the function increases in the intervals (
-
![]() ,
0
) and (
1, +
,
0
) and (
1, +
![]() )
and
)
and
decreases in the interval ( 0, 1 ). The point
x
= 0 isn’t included in the function
domain, but as
x
approaches 0 an item
x
-
2
increases unboundedly, therefore
the function also increases unboundedly. At the point
x
= 1 the function value
is 3. According to this analysis we can draw the graph of the function,
represented on Fig.4
b
.
Critical points. A domain interior points, in which a derivative of a function is equal to zero or doesn’t exist, are called critical points of this function. These points are very important at analysis and drawing a function graph, because only they can be points, in which a function has an extreme ( minimum or maximum , Fig.5 a, b ).
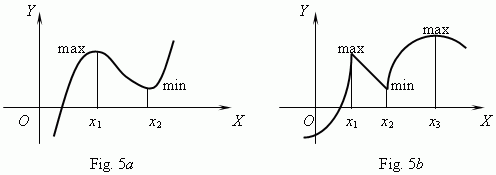
At points x 1 , x 2 ( Fig.5 a ) and x 3 ( Fig.5 b ) a derivative is equal to 0; at points x 1 , x 2 ( Fig.5 b ) a derivative doesn’t exist. But all they are points of extreme.
Necessary condition of extreme. If x 0 is an extreme point of a function f ( x ) and a derivative f’ exists at this point, then f’ ( x 0 ) = 0 .
This theorem is a necessary condition of extreme. If a derivative of a function at some point is equal to zero, then it’s not necessarily, that the function has an extreme at this point. For instance, a derivative of the function f ( x ) = x ³ is equal to 0 at x = 0 , but this function has no extreme at this point ( Fig.6 ).
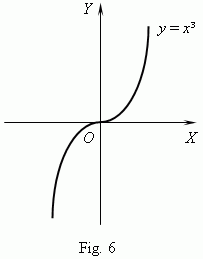
On the other hand, the function y = | x | , represented on Fig.3, has a minimum at the point x = 0 , but there is no derivative at this point.
Sufficient conditions of extreme. If a derivative changes its sign from plus to minus at a point x 0 , then x 0 is a point of maximum. If a derivative changes its sign from minus to plus at a point x 0 , then x 0 is a point of minimum.
Plan of function investigation. To draw a graph of a function it is necessary:
1) to find a domain and a codomain of a function,
2) to ascertain if the function is even or odd,
3) to determine if the function is periodic or not,
4) to find zeros of the function and its values at x = 0,
5) to find intervals of a sign constancy,
6) to find intervals of monotony,
7) to find points of extreme and values of a function in these points,
8) to analyze the behavior of a function near “special” points and at a great modulus of x .
E x a m p l e . Analyze the function f ( x ) = x ³ + 2 x ² - x - 2 and draw its graph.
S o l u t i o n . We’ll investigate the function by the above represented scheme.
1) a domain
x
![]() R
( i.e.
x
– any real number ); a codomain
y
R
( i.e.
x
– any real number ); a codomain
y
![]() R
,
because
R
,
because
f
(
x
) is an odd degree polynomial;
2)
f
(
x
) is neither an even nor an odd function ( explain, please );
3)
f
(
x
) is not a periodic function ( prove this, please, yourself );
4) a graph of this function is intersected with
y
-axis in the point ( 0,
-
2 ),
because
f
( 0 ) =
-
2 ; to find zeros of the function it is necessary to solve
the equation:
x
³
+ 2
x
²
-
x
-
2 = 0 , one of roots of which (
x
= 1 ) is
obvious. Other roots can be found ( if they exist ! ) by solving the quadratic
equation:
x
²
+ 3
x
+ 2 = 0, which is received after dividing the polynomial
x
³
+ 2
x
²
-
x
-
2 by the binomial (
x
– 1 ). It is easy to check, that the
two other roots are:
x
2
=
-
2 and
x
3
=
-
1. So, zeros of this function are:
-
2,
-
1 and 1.
5) It means, that a numerical line is divided by these roots into four intervals of
a sign constancy, inside of which the function saves
its sign :
This result can be received from the polynomial factorization:
x ³ + 2 x ² - x - 2 = ( x + 2 ) ( x + 1 ( x – 1 )
and estimating the product sign by the
method of intervals
.
6) The derivative:
f’
(
x
) = 3
x
²
+ 4
x
-
1 has no points, at which it doesn’t
exist, therefore its domain is
R
( all real numbers ); zeros of
f’
(
x
) are
roots of the equation: 3
x
²
+ 4
x
-
1 = 0 .
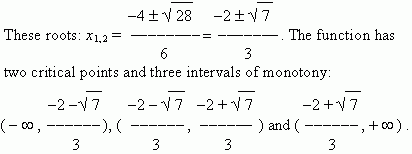
The received results are included in the following table: